 | ||
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.
Contents
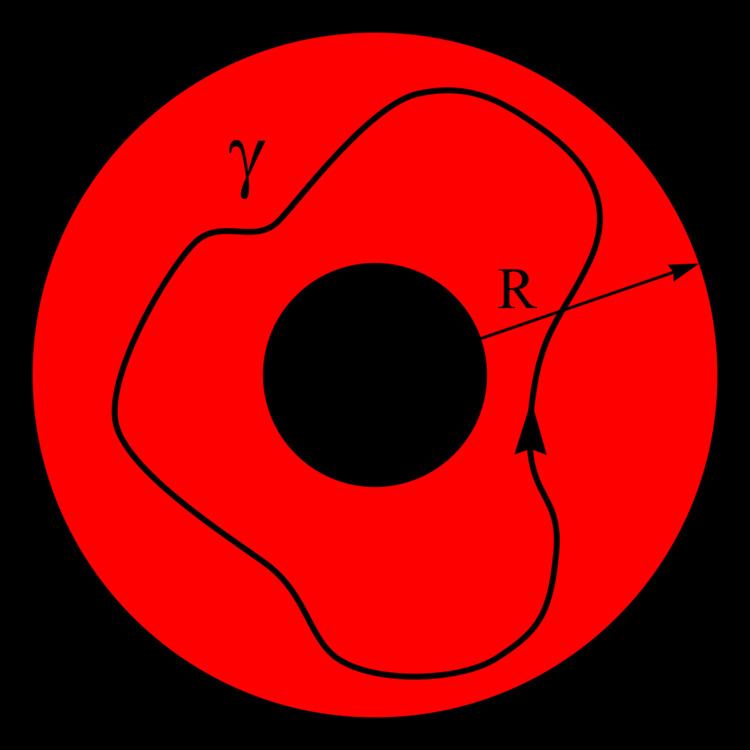
The Laurent series for a complex function f(z) about a point c is given by:
where the an and c are constants, defined by a line integral which is a generalization of Cauchy's integral formula:
The path of integration
In practice, the above integral formula may not offer the most practical method for computing the coefficients
Convergent Laurent series
Laurent series with complex coefficients are an important tool in complex analysis, especially to investigate the behavior of functions near singularities.
Consider for instance the function
for N = 1, 2, 3, 4, 5, 6, 7 and 50. As N → ∞, the approximation becomes exact for all (complex) numbers x except at the singularity x = 0.
More generally, Laurent series can be used to express holomorphic functions defined on an annulus, much as power series are used to express holomorphic functions defined on a disc.
Suppose
is a given Laurent series with complex coefficients an and a complex center c. Then there exists a unique inner radius r and outer radius R such that:
It is possible that r may be zero or R may be infinite; at the other extreme, it's not necessarily true that r is less than R. These radii can be computed as follows:
We take R to be infinite when this latter lim sup is zero.
Conversely, if we start with an annulus of the form A ≡ {z : r < |z − c| < R} and a holomorphic function ƒ(z) defined on A, then there always exists a unique Laurent series with center c which converges (at least) on A and represents the function ƒ(z).
As an example, consider the following rational function, along with its partial fraction expansion:
This function has singularities at z = 1 and z = 2i, where the denominator of the expression is zero and the expression is therefore undefined. A Taylor series about z = 0 (which yields a power series) will only converge in a disc of radius 1, since it "hits" the singularity at 1.
However, there are three possible Laurent expansions about 0, depending on the radius of z:
This follows from the partial fraction form of the function, along with the formula for the sum of a geometric series,
Here, we use the alternative form of the geometric series summation,
This series can be derived using geometric series as before, or by performing polynomial long division of 1 by (x−1)(x−2i), not stopping with a remainder but continuing into x−n terms; indeed, the "outer" Laurent series of a rational function is analogous to the decimal form of a fraction. (The "inner" Taylor series expansion can be obtained similarly, just reversing the term order in the division algorithm.)
The case r = 0; i.e., a holomorphic function ƒ(z) which may be undefined at a single point c, is especially important.
The coefficient a−1 of the Laurent expansion of such a function is called the residue of ƒ(z) at the singularity c; it plays a prominent role in the residue theorem.
For an example of this, consider
This function is holomorphic everywhere except at z = 0. To determine the Laurent expansion about c = 0, we use our knowledge of the Taylor series of the exponential function:
and we find that the residue is 2.
Uniqueness
Suppose a function ƒ(z) holomorphic on the annulus r < |z − c| < R has two Laurent series:
Multiply both sides with
The series converges uniformly on
into the summation yields
Hence the Laurent series is unique.
Laurent polynomials
A Laurent polynomial is a Laurent series in which only finitely many coefficients are non-zero. Laurent polynomials differ from ordinary polynomials in that they may have terms of negative degree.
Principal part
The principal part of a Laurent series is the series of terms with negative degree, that is
If the principal part of f is a finite sum, then f has a pole at c of order equal to (negative) the degree of the highest term; on the other hand, if f has an essential singularity at c, the principal part is an infinite sum (meaning it has infinitely many non-zero terms).
If the inner radius of convergence of the Laurent series for f is 0, then f has an essential singularity at c if and only if the principal part is an infinite sum, and has a pole otherwise.
If the inner radius of convergence is positive, f may have infinitely many negative terms but still be regular at c, as in the example above, in which case it is represented by a different Laurent series in a disk about c.
Laurent series with only finitely many negative terms are tame—they are a power series divided by
Multiplication
Laurent series cannot in general be multiplied. Algebraically, the expression for the terms of the product may involve infinite sums which need not converge (one cannot take the convolution of integer sequences). Geometrically, the two Laurent series may have non-overlapping annuli of convergence.
Two Laurent series with only finitely many negative terms can be multiplied: algebraically, the sums are all finite; geometrically, these have poles at c, and inner radius of convergence 0, so they both converge on an overlapping annulus.
Thus when defining formal Laurent series, one requires Laurent series with only finitely many negative terms.
Similarly, the sum of two convergent Laurent series need not converge, though it is always defined formally, but the sum of two bounded below Laurent series (or any Laurent series on a punctured disk) has a non-empty annulus of convergence.
