Latent Dirichlet allocation

Topics

In LDA, each document may be viewed as a mixture of various topics where each document is considered to have a set of topics that are assigned to it via LDA. This is similar to probabilistic latent semantic analysis (pLSA), except that in LDA the topic distribution is assumed to have a Dirichlet prior. In practice, this results in more reasonable mixtures of topics in a document. It has been noted, however, that the pLSA model is equivalent to the LDA model under a uniform Dirichlet prior distribution.

For example, an LDA model might have topics that can be classified as CAT_related and DOG_related. A topic has probabilities of generating various words, such as milk, meow, and kitten, which can be classified and interpreted by the viewer as "CAT_related". Naturally, the word cat itself will have high probability given this topic. The DOG_related topic likewise has probabilities of generating each word: puppy, bark, and bone might have high probability. Words without special relevance, such as the (see function word), will have roughly even probability between classes (or can be placed into a separate category). A topic is not strongly defined, neither semantically nor epistemologically. It is identified on the basis of supervised labeling and (manual) pruning on the basis of their likelihood of co-occurrence. A lexical word may occur in several topics with a different probability, however, with a different typical set of neighboring words in each topic.

Each document is assumed to be characterized by a particular set of topics. This is akin to the standard bag of words model assumption, and makes the individual words exchangeable.

Model

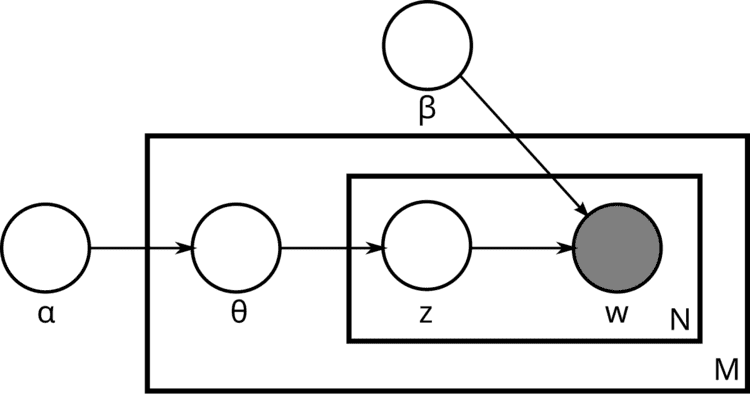
With plate notation, the dependencies among the many variables can be captured concisely. The boxes are “plates” representing replicates. The outer plate represents documents, while the inner plate represents the repeated choice of topics and words within a document. M denotes the number of documents, N the number of words in a document. Thus:

α is the parameter of the Dirichlet prior on the per-document topic distributions,β is the parameter of the Dirichlet prior on the per-topic word distribution, θ m is the topic distribution for document m, φ k is the word distribution for topic k, z m n is the topic for the n-th word in document m, and w m n is the specific word.

The w i j are the only observable variables, and the other variables are latent variables. Mostly, the basic LDA model will be extended to a smoothed version to gain better results . The plate notation is shown on the right, where K denotes the number of topics considered in the model and

φ is a K*V (V is the dimension of the vocabulary) Markov matrix (transition matrix), and each row of which denotes the word distribution of a topic.

Generative Process

The generative process is as follows. Documents are represented as random mixtures over latent topics, where each topic is characterized by a distribution over words. LDA assumes the following generative process for a corpus D consisting of M documents each of length N i :

1. Choose θ i ∼ D i r ( α ) , where i ∈ { 1 , … , M } and D i r ( α ) is the Dirichlet distribution for parameter α

2. Choose φ k ∼ D i r ( β ) , where k ∈ { 1 , … , K }

3. For each of the word positions i , j , where j ∈ { 1 , … , N i } , and i ∈ { 1 , … , M }

(a) Choose a topic z i , j ∼ M u l t i n o m i a l ( θ i ) . (b) Choose a word w i , j ∼ M u l t i n o m i a l ( φ z i , j ) .

(Note that the Multinomial distribution here refers to the Multinomial with only one trial. It is formally equivalent to the categorical distribution.)

The lengths N i are treated as independent of all the other data generating variables ( w and z ). The subscript is often dropped, as in the plate diagrams shown here.

Definition

A formal description of smoothed LDA is as follows:

We can then mathematically describe the random variables as follows:

φ k = 1 … K ∼ Dirichlet V ⁡ ( β ) θ d = 1 … M ∼ Dirichlet K ⁡ ( α ) z d = 1 … M , w = 1 … N d ∼ Categorical K ⁡ ( θ d ) w d = 1 … M , w = 1 … N d ∼ Categorical V ⁡ ( φ z d w )

Inference

Learning the various distributions (the set of topics, their associated word probabilities, the topic of each word, and the particular topic mixture of each document) is a problem of Bayesian inference. The original paper used a variational Bayes approximation of the posterior distribution; alternative inference techniques use Gibbs sampling and expectation propagation.

Following is the derivation of the equations for collapsed Gibbs sampling, which means φ s and θ s will be integrated out. For simplicity, in this derivation the documents are all assumed to have the same length N . The derivation is equally valid if the document lengths vary.

According to the model, the total probability of the model is:

P ( W , Z , θ , φ ; α , β ) = ∏ i = 1 K P ( φ i ; β ) ∏ j = 1 M P ( θ j ; α ) ∏ t = 1 N P ( Z j , t | θ j ) P ( W j , t | φ Z j , t ) ,

where the bold-font variables denote the vector version of the variables. First, φ and θ need to be integrated out.

P ( Z , W ; α , β ) = ∫ θ ∫ φ P ( W , Z , θ , φ ; α , β ) d φ d θ = ∫ φ ∏ i = 1 K P ( φ i ; β ) ∏ j = 1 M ∏ t = 1 N P ( W j , t ∣ φ Z j , t ) d φ ∫ θ ∏ j = 1 M P ( θ j ; α ) ∏ t = 1 N P ( Z j , t ∣ θ j ) d θ .

All the θ s are independent to each other and the same to all the φ s. So we can treat each θ and each φ separately. We now focus only on the θ part.

∫ θ ∏ j = 1 M P ( θ j ; α ) ∏ t = 1 N P ( Z j , t ∣ θ j ) d θ = ∏ j = 1 M ∫ θ j P ( θ j ; α ) ∏ t = 1 N P ( Z j , t ∣ θ j ) d θ j .

We can further focus on only one θ as the following:

∫ θ j P ( θ j ; α ) ∏ t = 1 N P ( Z j , t ∣ θ j ) d θ j .

Actually, it is the hidden part of the model for the j t h document. Now we replace the probabilities in the above equation by the true distribution expression to write out the explicit equation.

∫ θ j P ( θ j ; α ) ∏ t = 1 N P ( Z j , t ∣ θ j ) d θ j = ∫ θ j Γ ( ∑ i = 1 K α i ) ∏ i = 1 K Γ ( α i ) ∏ i = 1 K θ j , i α i − 1 ∏ t = 1 N P ( Z j , t ∣ θ j ) d θ j .

Let n j , r i be the number of word tokens in the j t h document with the same word symbol (the r t h word in the vocabulary) assigned to the i t h topic. So, n j , r i is three dimensional. If any of the three dimensions is not limited to a specific value, we use a parenthesized point ( ⋅ ) to denote. For example, n j , ( ⋅ ) i denotes the number of word tokens in the j t h document assigned to the i t h topic. Thus, the right most part of the above equation can be rewritten as:

∏ t = 1 N P ( Z j , t ∣ θ j ) = ∏ i = 1 K θ j , i n j , ( ⋅ ) i .

So the θ j integration formula can be changed to:

∫ θ j Γ ( ∑ i = 1 K α i ) ∏ i = 1 K Γ ( α i ) ∏ i = 1 K θ j , i α i − 1 ∏ i = 1 K θ j , i n j , ( ⋅ ) i d θ j = ∫ θ j Γ ( ∑ i = 1 K α i ) ∏ i = 1 K Γ ( α i ) ∏ i = 1 K θ j , i n j , ( ⋅ ) i + α i − 1 d θ j .

Clearly, the equation inside the integration has the same form as the Dirichlet distribution. According to the Dirichlet distribution,

∫ θ j Γ ( ∑ i = 1 K n j , ( ⋅ ) i + α i ) ∏ i = 1 K Γ ( n j , ( ⋅ ) i + α i ) ∏ i = 1 K θ j , i n j , ( ⋅ ) i + α i − 1 d θ j = 1.

Thus,

∫ θ j P ( θ j ; α ) ∏ t = 1 N P ( Z j , t ∣ θ j ) d θ j = ∫ θ j Γ ( ∑ i = 1 K α i ) ∏ i = 1 K Γ ( α i ) ∏ i = 1 K θ j , i n j , ( ⋅ ) i + α i − 1 d θ j = Γ ( ∑ i = 1 K α i ) ∏ i = 1 K Γ ( α i ) ∏ i = 1 K Γ ( n j , ( ⋅ ) i + α i ) Γ ( ∑ i = 1 K n j , ( ⋅ ) i + α i ) ∫ θ j Γ ( ∑ i = 1 K n j , ( ⋅ ) i + α i ) ∏ i = 1 K Γ ( n j , ( ⋅ ) i + α i ) ∏ i = 1 K θ j , i n j , ( ⋅ ) i + α i − 1 d θ j = Γ ( ∑ i = 1 K α i ) ∏ i = 1 K Γ ( α i ) ∏ i = 1 K Γ ( n j , ( ⋅ ) i + α i ) Γ ( ∑ i = 1 K n j , ( ⋅ ) i + α i ) .

Now we turn our attentions to the φ part. Actually, the derivation of the φ part is very similar to the θ part. Here we only list the steps of the derivation:

∫ φ ∏ i = 1 K P ( φ i ; β ) ∏ j = 1 M ∏ t = 1 N P ( W j , t ∣ φ Z j , t ) d φ = ∏ i = 1 K ∫ φ i P ( φ i ; β ) ∏ j = 1 M ∏ t = 1 N P ( W j , t ∣ φ Z j , t ) d φ i = ∏ i = 1 K ∫ φ i Γ ( ∑ r = 1 V β r ) ∏ r = 1 V Γ ( β r ) ∏ r = 1 V φ i , r β r − 1 ∏ r = 1 V φ i , r n ( ⋅ ) , r i d φ i = ∏ i = 1 K ∫ φ i Γ ( ∑ r = 1 V β r ) ∏ r = 1 V Γ ( β r ) ∏ r = 1 V φ i , r n ( ⋅ ) , r i + β r − 1 d φ i = ∏ i = 1 K Γ ( ∑ r = 1 V β r ) ∏ r = 1 V Γ ( β r ) ∏ r = 1 V Γ ( n ( ⋅ ) , r i + β r ) Γ ( ∑ r = 1 V n ( ⋅ ) , r i + β r ) .

For clarity, here we write down the final equation with both ϕ and θ integrated out:

P ( Z , W ; α , β ) = ∏ j = 1 M Γ ( ∑ i = 1 K α i ) ∏ i = 1 K Γ ( α i ) ∏ i = 1 K Γ ( n j , ( ⋅ ) i + α i ) Γ ( ∑ i = 1 K n j , ( ⋅ ) i + α i ) × ∏ i = 1 K Γ ( ∑ r = 1 V β r ) ∏ r = 1 V Γ ( β r ) ∏ r = 1 V Γ ( n ( ⋅ ) , r i + β r ) Γ ( ∑ r = 1 V n ( ⋅ ) , r i + β r ) .

The goal of Gibbs Sampling here is to approximate the distribution of P ( Z ∣ W ; α , β ) . Since P ( W ; α , β ) is invariable for any of Z, Gibbs Sampling equations can be derived from P ( Z , W ; α , β ) directly. The key point is to derive the following conditional probability:

P ( Z ( m , n ) ∣ Z − ( m , n ) , W ; α , β ) = P ( Z ( m , n ) , Z − ( m , n ) , W ; α , β ) P ( Z − ( m , n ) , W ; α , β ) ,

where Z ( m , n ) denotes the Z hidden variable of the n t h word token in the m t h document. And further we assume that the word symbol of it is the v t h word in the vocabulary. Z − ( m , n ) denotes all the Z s but Z ( m , n ) . Note that Gibbs Sampling needs only to sample a value for Z ( m , n ) , according to the above probability, we do not need the exact value of

P ( Z m , n ∣ Z − ( m , n ) , W ; α , β )

but the ratios among the probabilities that Z ( m , n ) can take value. So, the above equation can be simplified as:

P ( Z ( m , n ) = k ∣ Z − ( m , n ) , W ; α , β ) ∝ P ( Z ( m , n ) = k , Z − ( m , n ) , W ; α , β ) = ( Γ ( ∑ i = 1 K α i ) ∏ i = 1 K Γ ( α i ) ) M ∏ j ≠ m ∏ i = 1 K Γ ( n j , ( ⋅ ) i + α i ) Γ ( ∑ i = 1 K n j , ( ⋅ ) i + α i ) ( Γ ( ∑ r = 1 V β r ) ∏ r = 1 V Γ ( β r ) ) K ∏ i = 1 K ∏ r ≠ v Γ ( n ( ⋅ ) , r i + β r ) ∏ i = 1 K Γ ( n m , ( ⋅ ) i + α i ) Γ ( ∑ i = 1 K n m , ( ⋅ ) i + α i ) ∏ i = 1 K Γ ( n ( ⋅ ) , v i + β v ) Γ ( ∑ r = 1 V n ( ⋅ ) , r i + β r ) ∝ ∏ i = 1 K Γ ( n m , ( ⋅ ) i + α i ) Γ ( ∑ i = 1 K n m , ( ⋅ ) i + α i ) ∏ i = 1 K Γ ( n ( ⋅ ) , v i + β v ) Γ ( ∑ r = 1 V n ( ⋅ ) , r i + β r ) ∝ ∏ i = 1 K Γ ( n m , ( ⋅ ) i + α i ) ∏ i = 1 K Γ ( n ( ⋅ ) , v i + β v ) Γ ( ∑ r = 1 V n ( ⋅ ) , r i + β r ) .

Finally, let n j , r i , − ( m , n ) be the same meaning as n j , r i but with the Z ( m , n ) excluded. The above equation can be further simplified leveraging the property of gamma function. We first split the summation and then merge it back to obtain a k -independent summation, which could be dropped:

∝ ∏ i ≠ k Γ ( n m , ( ⋅ ) i , − ( m , n ) + α i ) ∏ i ≠ k Γ ( n ( ⋅ ) , v i , − ( m , n ) + β v ) Γ ( ∑ r = 1 V n ( ⋅ ) , r i , − ( m , n ) + β r ) Γ ( n m , ( ⋅ ) k , − ( m , n ) + α k + 1 ) Γ ( n ( ⋅ ) , v k , − ( m , n ) + β v + 1 ) Γ ( ∑ r = 1 V n ( ⋅ ) , r k , − ( m , n ) + β r + 1 ) = ∏ i ≠ k Γ ( n m , ( ⋅ ) i , − ( m , n ) + α i ) ∏ i ≠ k Γ ( n ( ⋅ ) , v i , − ( m , n ) + β v ) Γ ( ∑ r = 1 V n ( ⋅ ) , r i , − ( m , n ) + β r ) Γ ( n m , ( ⋅ ) k , − ( m , n ) + α k ) Γ ( n ( ⋅ ) , v k , − ( m , n ) + β v ) Γ ( ∑ r = 1 V n ( ⋅ ) , r k , − ( m , n ) + β r ) ( n m , ( ⋅ ) k , − ( m , n ) + α k ) n ( ⋅ ) , v k , − ( m , n ) + β v ∑ r = 1 V n ( ⋅ ) , r k , − ( m , n ) + β r = ∏ i Γ ( n m , ( ⋅ ) i , − ( m , n ) + α i ) ∏ i Γ ( n ( ⋅ ) , v i , − ( m , n ) + β v ) Γ ( ∑ r = 1 V n ( ⋅ ) , r i , − ( m , n ) + β r ) ( n m , ( ⋅ ) k , − ( m , n ) + α k ) n ( ⋅ ) , v k , − ( m , n ) + β v ∑ r = 1 V n ( ⋅ ) , r k , − ( m , n ) + β r ∝ ( n m , ( ⋅ ) k , − ( m , n ) + α k ) n ( ⋅ ) , v k , − ( m , n ) + β v ∑ r = 1 V n ( ⋅ ) , r k , − ( m , n ) + β r

Note that the same formula is derived in the article on the Dirichlet-multinomial distribution, as part of a more general discussion of integrating Dirichlet distribution priors out of a Bayesian network.

Faster sampling

Recent research has been focused on speeding up the inference of latent Dirichlet Allocation to support capture of a massive number of topics in large number of documents. The update equation of the collapsed Gibbs sampler mentioned in the earlier section has a natural sparsity within it that can be taken advantage of. Intuitively, since each document only contains a subset of topics K d , and a word also only appears in a subset of topics K w , the above update equation could be rewritten to take advantage of this sparsity.

p ( Z d , n = k ) ∝ α β C k ¬ n + V β + C k d β C k ¬ n + V β + C k w ( α + C k d ) C k ¬ n + V β

In this equation, we have three terms, out of which two of them are sparse, and the other is small. We call these terms a , b and c respectively. Now, if we normalize each term by summing over all the topics, we get:

A = ∑ k = 1 K α β C k ¬ n + V β

B = ∑ k = 1 K C k d β C k ¬ n + V β

C = ∑ k = 1 K C k w ( α + C k d ) C k ¬ n + V β

Here, we can see that B is a summation of the topics that appear in document d , and C is also a sparse summation of the topics that a word w has been observed by in the whole corpus. A on the other hand, is dense but because of the small values of α & β , the value is very small compared to the two other terms.

Now, while sampling a topic, if we sample a random variable uniformly from s ∼ U ( s | A + B + C ) , we can check which bucket our sample lands in. Since A is small, we are very unlikely to fall into this bucket; however, if we do fall into this bucket, sampling a topic takes O(K) time (same as the original Collapsed Gibbs Sampler). However, if we fall into the other two buckets, we only need to check a subset of topics if we keep record of the sparse topics. A topic can be sampled from the B bucket in O ( K d ) time, and a topic can be sampled in O ( K w + K d ) time.

Notice that after sampling each topic, updating these buckets are all basic O ( 1 ) arithmetic operations.

Applications, extensions and similar techniques

Topic modeling is a classic problem in information retrieval. Related models and techniques are, among others, latent semantic indexing, independent component analysis, probabilistic latent semantic indexing, non-negative matrix factorization, and Gamma-Poisson distribution.

The LDA model is highly modular and can therefore be easily extended. The main field of interest is modeling relations between topics. This is achieved by using another distribution on the simplex instead of the Dirichlet. The Correlated Topic Model follows this approach, inducing a correlation structure between topics by using the logistic normal distribution instead of the Dirichlet. Another extension is the hierarchical LDA (hLDA), where topics are joined together in a hierarchy by using the nested Chinese restaurant process. LDA can also be extended to a corpus in which a document includes two types of information (e.g., words and names), as in the LDA-dual model. Nonparametric extensions of LDA include the hierarchical Dirichlet process mixture model, which allows the number of topics to be unbounded and learnt from data and the nested Chinese restaurant process which allows topics to be arranged in a hierarchy whose structure is learnt from data.

As noted earlier, pLSA is similar to LDA. The LDA model is essentially the Bayesian version of pLSA model. The Bayesian formulation tends to perform better on small datasets because Bayesian methods can avoid overfitting the data. For very large datasets, the results of the two models tend to converge. One difference is that pLSA uses a variable d to represent a document in the training set. So in pLSA, when presented with a document the model hasn't seen before, we fix Pr ( w ∣ z ) —the probability of words under topics—to be that learned from the training set and use the same EM algorithm to infer Pr ( z ∣ d ) —the topic distribution under d . Blei argues that this step is cheating because you are essentially refitting the model to the new data.

Variations on LDA have been used to automatically put natural images into categories, such as "bedroom" or "forest", by treating an image as a document, and small patches of the image as words; one of the variations is called Spatial Latent Dirichlet Allocation.

Recently, LDA has been also applied to bioinformatics context.

LDA is often prone to creating topics that are not easily interpretable by humans. Recent extensions include generating topics from a user-defined seed set of keywords.