Jensen's inequality

Statements

The classical form of Jensen's inequality involves several numbers and weights. The inequality can be stated quite generally using either the language of measure theory or (equivalently) probability. In the probabilistic setting, the inequality can be further generalized to its full strength.

Finite form

For a real convex function φ , numbers x 1 , x 2 , … , x n in its domain, and positive weights a i , Jensen's inequality can be stated as:

and the inequality is reversed if φ is concave, which is

Equality holds if and only if x 1 = x 2 = ⋯ = x n or φ is linear.

As a particular case, if the weights a i are all equal, then (1) and (2) become

For instance, the function log(x) is concave, so substituting φ ( x ) = log ⁡ ( x ) in the previous formula (4) establishes the (logarithm of the) familiar arithmetic mean-geometric mean inequality:

A common application has x as a function of another variable (or set of variables) t , that is, x i = g ( t i ) . All of this carries directly over to the general continuous case: the weights a_i are replaced by a non-negative integrable function  f (x), such as a probability distribution, and the summations are replaced by integrals.

Measure-theoretic and probabilistic form

Let ( Ω , A , μ ) be a probability space, such that μ ( Ω ) = 1 . If g is a real-valued function that is μ -integrable, and if φ is a convex function on the real line, then:

In real analysis, we may require an estimate on

where a , b ∈ R , and f : [ a , b ] → R is a non-negative Lebesgue-integrable function. In this case, the Lebesgue measure of [ a , b ] need not be unity. However, by integration by substitution, the interval can be rescaled so that it has measure unity. Then Jensen's inequality can be applied to get

The same result can be equivalently stated in a probability theory setting, by a simple change of notation. Let ( Ω , F , P ) be a probability space, X an integrable real-valued random variable and φ a convex function. Then:

In this probability setting, the measure μ is intended as a probability P , the integral with respect to μ as an expected value E , and the function g as a random variable X.

Notice that the equality holds if X is constant (degenerate random variable) or if φ is linear, and even if there is A ⊂ R (a Borel set, in fact) such that

and φ is a linear function over A (that is, there are a , b ∈ R such that φ ( x ) = a x + b , ∀ x ∈ A ).

General inequality in a probabilistic setting

More generally, let T be a real topological vector space, and X a T-valued integrable random variable. In this general setting, integrable means that there exists an element E [ X ] in T, such that for any element z in the dual space of T: E | ⟨ z , X ⟩ | < ∞ , and ⟨ z , E [ X ] ⟩ = E [ ⟨ z , X ⟩ ] . Then, for any measurable convex function φ and any sub-σ-algebra G of F :

Here E [ ⋅ ∣ G ] stands for the expectation conditioned to the σ-algebra G . This general statement reduces to the previous ones when the topological vector space T is the real axis, and G is the trivial σ-algebra {∅, Ω}.

Proofs

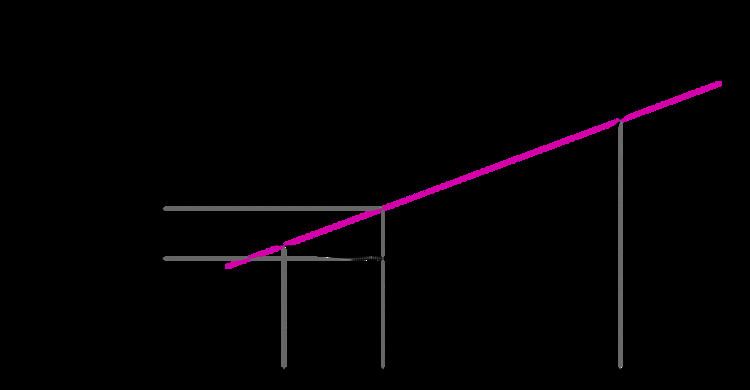
Jensen's inequality can be proved in several ways, and three different proofs corresponding to the different statements above will be offered. Before embarking on these mathematical derivations, however, it is worth analyzing an intuitive graphical argument based on the probabilistic case where X is a real number (see figure). Assuming a hypothetical distribution of X values, one can immediately identify the position of E [ X ] and its image φ ( E [ X ] ) in the graph. Noticing that for convex mappings Y = φ(X) the corresponding distribution of Y values is increasingly "stretched out" for increasing values of X, it is easy to see that the distribution of Y is broader in the interval corresponding to X > X₀ and narrower in X < X₀ for any X₀; in particular, this is also true for X 0 = E [ X ] . Consequently, in this picture the expectation of Y will always shift upwards with respect to the position of φ ( E [ X ] ) . A similar reasoning holds if the distribution of X covers a decreasing portion of the convex function, or both a decreasing and an increasing portion of it. This "proves" the inequality, i.e.

with equality when φ(X) is not strictly convex, e.g. when it is a straight line, or when X follows a degenerate distribution (i.e. is a constant).

The proofs below formalize this intuitive notion.

Proof 1 (finite form)

If λ₁ and λ₂ are two arbitrary nonnegative real numbers such that λ₁ + λ₂ = 1 then convexity of φ implies

This can be easily generalized: if λ₁, ..., λ_n are nonnegative real numbers such that λ₁ + ... + λ_n = 1, then

for any x₁, ..., x_n. This finite form of the Jensen's inequality can be proved by induction: by convexity hypotheses, the statement is true for n = 2. Suppose it is true also for some n, one needs to prove it for n + 1. At least one of the λ_i is strictly positive, say λ₁; therefore by convexity inequality:

Since

one can apply the induction hypotheses to the last term in the previous formula to obtain the result, namely the finite form of the Jensen's inequality.

In order to obtain the general inequality from this finite form, one needs to use a density argument. The finite form can be rewritten as:

where μ_n is a measure given by an arbitrary convex combination of Dirac deltas:

Since convex functions are continuous, and since convex combinations of Dirac deltas are weakly dense in the set of probability measures (as could be easily verified), the general statement is obtained simply by a limiting procedure.

Proof 2 (measure-theoretic form)

Let g be a real-valued μ-integrable function on a probability space Ω, and let φ be a convex function on the real numbers. Since φ is convex, at each real number x we have a nonempty set of subderivatives, which may be thought of as lines touching the graph of φ at x, but which are at or below the graph of φ at all points.

Now, if we define

because of the existence of subderivatives for convex functions, we may choose a and b such that

for all real x and

But then we have that

for all x. Since we have a probability measure, the integral is monotone with μ(Ω) = 1 so that

as desired.

Proof 3 (general inequality in a probabilistic setting)

Let X be an integrable random variable that takes values in a real topological vector space T. Since ϕ : T → R is convex, for any x , y ∈ T , the quantity

is decreasing as θ approaches 0⁺. In particular, the subdifferential of φ evaluated at x in the direction y is well-defined by

It is easily seen that the subdifferential is linear in y (that is false and the assertion requires Hahn-Banach theorem to be proved) and, since the infimum taken in the right-hand side of the previous formula is smaller than the value of the same term for θ = 1, one gets

In particular, for an arbitrary sub-σ-algebra G we can evaluate the last inequality when x = E [ X ∣ G ] , y = X − E [ X ∣ G ] to obtain

Now, if we take the expectation conditioned to G on both sides of the previous expression, we get the result since:

by the linearity of the subdifferential in the y variable, and the following well-known property of the conditional expectation:

Form involving a probability density function

Suppose Ω is a measurable subset of the real line and f(x) is a non-negative function such that

In probabilistic language, f is a probability density function.

Then Jensen's inequality becomes the following statement about convex integrals:

If g is any real-valued measurable function and φ is convex over the range of g, then

If g(x) = x, then this form of the inequality reduces to a commonly used special case:

Alternative finite form

Let Ω = {x₁, ... x_n}, and take μ to be the counting measure on Ω, then the general form reduces to a statement about sums:

provided that λ_i ≥ 0 and

There is also an infinite discrete form.

Statistical physics

Jensen's inequality is of particular importance in statistical physics when the convex function is an exponential, giving:

where the expected values are with respect to some probability distribution in the random variable X.

The proof in this case is very simple (cf. Chandler, Sec. 5.5). The desired inequality follows directly, by writing

and then applying the inequality e^X ≥ 1 + X to the final exponential.

Information theory

If p(x) is the true probability distribution for x, and q(x) is another distribution, then applying Jensen's inequality for the random variable Y(x) = q(x)/p(x) and the function φ(y) = −log(y) gives

Therefore:

a result called Gibbs' inequality.

It shows that the average message length is minimised when codes are assigned on the basis of the true probabilities p rather than any other distribution q. The quantity that is non-negative is called the Kullback–Leibler divergence of q from p.

Since −log(x) is a strictly convex function for x > 0, it follows that equality holds when p(x) equals q(x) almost everywhere.

Rao–Blackwell theorem

If L is a convex function and G a sub-sigma-algebra, then, from the conditional version of Jensen's inequality, we get

So if δ(X) is some estimator of an unobserved parameter θ given a vector of observables X; and if T(X) is a sufficient statistic for θ; then an improved estimator, in the sense of having a smaller expected loss L, can be obtained by calculating

the expected value of δ with respect to θ, taken over all possible vectors of observations X compatible with the same value of T(X) as that observed.

This result is known as the Rao–Blackwell theorem.