 | ||
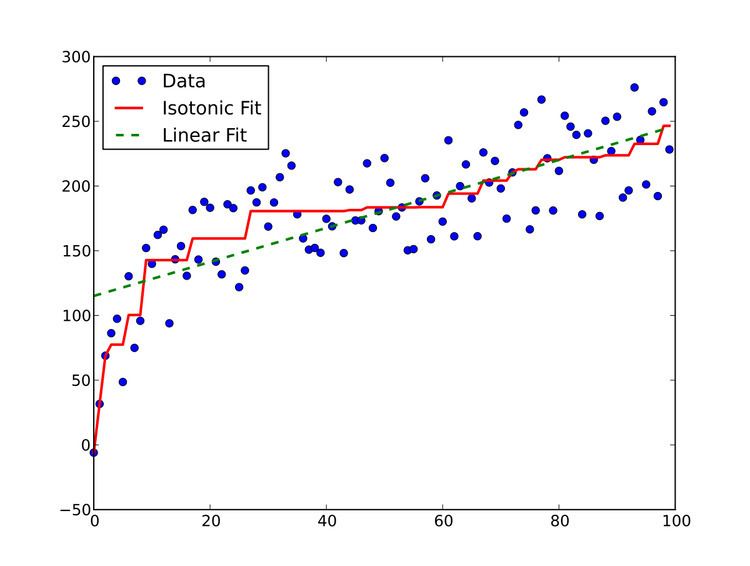
In statistics, isotonic regression or monotonic regression is the technique of fitting a free-form line to a sequence of observations under the following constraints: the fitted free-form line has to be non-decreasing everywhere, and it has to lie as close to the observations as possible.
Contents
Applications
Isotonic regression has applications in statistical inference, for example, to fit of an isotonic curve to mean experimental results when an order is expected. A benefit of isotonic regression is that it does not assume any form for the target function, such as linearity assumed by linear regression.
Another application is nonmetric multidimensional scaling, where a low-dimensional embedding for data points is sought such that order of distances between points in the embedding matches order of dissimilarity between points. Isotonic regression is used iteratively to fit ideal distances to preserve relative dissimilarity order.
Software for computing isotone (monotonic) regression has been developed for the R statistical package and the Python programming language.
Algorithms
In terms of numerical analysis, isotonic regression involves finding a weighted least-squares fit
Such constraints define a partial ordering or total ordering and can be represented as a directed graph
In the case when
Simply ordered case
To illustrate the above, let the
The isotonic estimator,
where
