Integral of inverse functions

Statement of the theorem

Let I 1 and I 2 be two intervals of R . Assume that f : I 1 → I 2 is a continuous and invertible function, and let f − 1 denote its inverse I 2 → I 1 . Then f and f − 1 have antiderivatives, and if F is an antiderivative of f , the possible antiderivatives of f − 1 are:

where C is an arbitrary real number.

In his 1905 article, Laisant gave three proofs. First, under the additional hypothesis that f − 1 is differentiable, one may differentiate the above formula, which completes the proof immediately. His second proof was geometric. If f ( a ) = c and f ( b ) = d , the theorem can be written:

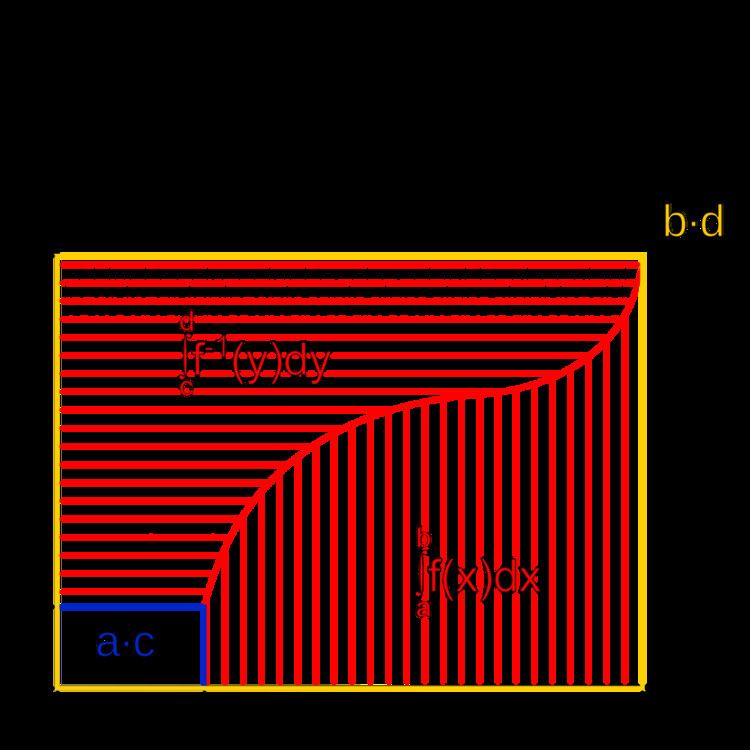
The figure on the right is a proof without words of this formula. Laisant does not discuss the hypotheses necessary to make this proof rigorous, but it can be made explicit with the help of the Darboux integral (or Fubini's theorem if a demonstration based on the Lebesgue integral is desired). Laisant's third proof uses the additional hypothesis that f is differentiable. Beginning with f − 1 ( f ( x ) ) = x , one multiplies by f ′ ( x ) and integrates both sides. The right-hand side is calculated using integration by parts to be x f ( x ) − ∫ f ( x ) d x , and the formula follows.

Nevertheless, it can be shown that this theorem holds even if f or f − 1 is not differentiable: it suffices, for example, to use the Stieltjes integral in the previous argument. On the other hand, even though general monotonic functions are differentiable almost everywhere, the proof of the general formula does not follow, unless f − 1 is absolutely continuous.

It is also possible to check that for every y in I 2 , the derivative of the function y → y f − 1 ( y ) − F ( f − 1 ( y ) ) is equal to f − 1 ( y ) . In other words:

To this end, it suffices to apply the mean value theorem to F between x and x + h , taking into account that f is monotonic.

Examples

1. Assume that f ( x ) = exp ⁡ ( x ) , hence f − 1 ( y ) = ln ⁡ ( y ) . The formula above gives immediately
   ∫ ln ⁡ ( y ) d y = y ln ⁡ ( y ) − y + C .
2. Similarly, with f ( x ) = cos ⁡ ( x ) and f − 1 ( y ) = arccos ⁡ ( y ) ,
   ∫ arccos ⁡ ( y ) d y = y arccos ⁡ ( y ) − sin ⁡ ( arccos ⁡ ( y ) ) + C .
3. With f ( x ) = tan ⁡ ( x ) and f − 1 ( y ) = arctan ⁡ ( y ) ,
   ∫ arctan ⁡ ( y ) d y = y arctan ⁡ ( y ) + ln ⁡ | cos ⁡ ( arctan ⁡ ( y ) ) | + C .

History

Apparently, this theorem of integration was discovered for the first time in 1905 by Charles-Ange Laisant, who "could hardly believe that this theorem is new", and hoped its use would henceforth spread out among students and teachers. This result was published independently in 1912 by an Italian engineer, Alberto Caprilli, in an opuscule entitled "Nuove formole d'integrazione". It was rediscovered in 1955 by Parker, and by a number of mathematicians following him. Nevertheless, they all assume that f or f⁻¹ is differentiable. The general version of the theorem, free from this additional assumption, was proposed by Michael Spivak in 1965, as an exercise in the Calculus, and a fairly complete proof following the same lines was published by Eric Key in 1994. This proof relies on the very definition of the Darboux integral, and consists in showing that the upper Darboux sums of the function f are in 1-1 correspondence with the lower Darboux sums of f⁻¹. In 2013, Michael Bensimhoun, estimating that the general theorem was still insufficiently known, gave two other proofs: The second proof, based on the Stieltjes integral and on its formulae of integration by parts and of homeomorphic change of variables, is the most suitable to establish more complex formulae.

Generalization to holomorphic functions

The above theorem generalizes in the obvious way to holomorphic functions: Let U and V be two open and simply connected sets of C , and assume that f : U → V is a biholomorphism. Then f and f − 1 have antiderivatives, and if F is an antiderivative of f , the general antiderivative of f − 1 is

Because all holomorphic functions are differentiable, the proof is immediate by complex differentiation.