 | ||
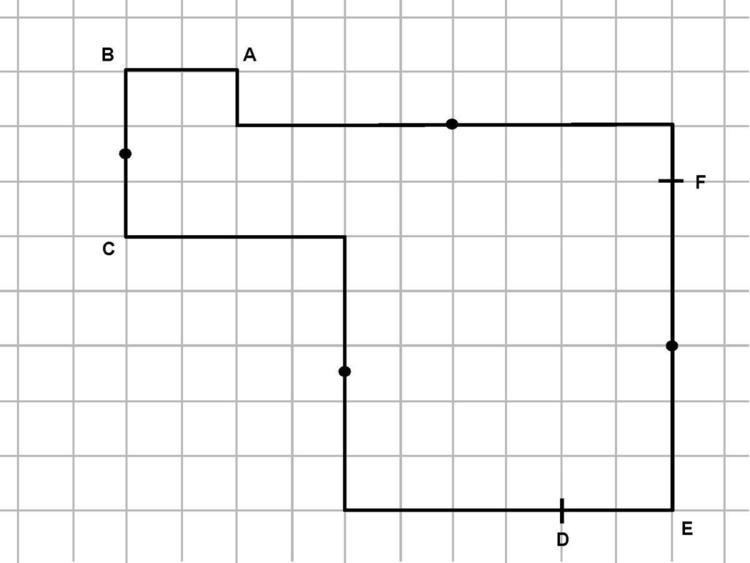
In the mathematical theory of tessellations, the Conway criterion, named for the English mathematician John Horton Conway, describes rules for when a prototile will tile the plane; it consists of the following requirements: The tile must be a closed topological disk with six consecutive points A, B, C, D, E, and F on the boundary such that:
Any prototile satisfying Conway's criterion admits a periodic tiling of the plane—and does so using only translation and 180-degree rotations. The Conway criterion is a sufficient condition to prove that a prototile tiles the plane but not a necessary one; there are tiles that fail the criterion and still tile the plane.
Examples
In its simplest form the criterion states that any hexagon with a pair of opposite sides that are parallel and congruent will tessellate the plane by translation, called hexagonal parallelogons. But when some of the points coincide, the criterion can apply to other polygons and even to shapes with curved perimeters.
The Conway criterion discriminates many shapes, especially polyforms: except the two tiling nonominoes on the right, all tiling polyominos up to the nonominoes can form a patch of at least one tile which satisfies the criterion. These figures also show that the criterion is a sufficient but not necessary condition for a prototile to tile the plane.
