Finite potential well

Particle in a 1-dimensional box

For the 1-dimensional case on the x-axis, the time-independent Schrödinger equation can be written as:

− ℏ 2 2 m d 2 ψ d x 2 + V ( x ) ψ = E ψ ( 1 )

where

ℏ = h 2 π , h is Planck's constant, m is the mass of the particle, ψ is the (complex valued) wavefunction that we want to find, V ( x ) is a function describing the potential energy at each point x, and E is the energy, a real number, sometimes called eigenenergy.

For the case of the particle in a 1-dimensional box of length L, the potential is zero inside the box, but rises abruptly to a value V o at x = -L/2 and x = L/2. The wavefunction is considered to be made up of different wavefuctions at different ranges of x, depending on whether x is inside or outside of the box. Therefore, the wavefunction is defined such that:

ψ = { ψ 1 , if  x < − L / 2  (the region outside the box) ψ 2 , if  − L / 2 < x < L / 2  (the region inside the box) ψ 3 if  x > L / 2  (the region outside the box)

Inside the box

For the region inside the box V(x) = 0 and Equation 1 reduces to

− ℏ 2 2 m d 2 ψ 2 d x 2 = E ψ 2 .

Letting

k = 2 m E ℏ ,

the equation becomes

d 2 ψ 2 d x 2 = − k 2 ψ 2 .

This is a well-studied differential equation and eigenvalue problem with a general solution of

ψ 2 = A sin ⁡ ( k x ) + B cos ⁡ ( k x ) .

Hence,

E = k 2 ℏ 2 2 m .

Here, A and B can be any complex numbers, and k can be any real number.

Outside the box

For the region outside of the box, since the potential is constant, V(x) = V o and Equation 1 becomes:

− ℏ 2 2 m d 2 ψ 1 d x 2 = ( E − V o ) ψ 1

There are two possible families of solutions, depending on whether E is less than V o (the particle is bound in the potential) or E is greater than V o (the particle is free).

For a free particle, E > V o , and letting

k ′ = 2 m ( E − V o ) ℏ

produces

d 2 ψ 1 d x 2 = − k ′ 2 ψ 1

with the same solution form as the inside-well case:

ψ 1 = C sin ⁡ ( k ′ x ) + D cos ⁡ ( k ′ x )

This analysis will focus on the bound state, where V o > E. Letting

α = 2 m ( V o − E ) ℏ

produces

d 2 ψ 1 d x 2 = α 2 ψ 1

where the general solution is exponential:

ψ 1 = F e − α x + G e α x

Similarly, for the other region outside the box:

ψ 3 = H e − α x + I e α x

Now in order to find the specific solution for the problem at hand, we must specify the appropriate boundary conditions and find the values for A, B, F, G, H and I that satisfy those conditions.

Finding wavefunctions for the bound state

Solutions to the Schrödinger equation must be continuous, and continuously differentiable. These requirements are boundary conditions on the differential equations previously derived.

In this case, the finite potential well is symmetrical, so symmetry can be exploited to reduce the necessary calculations.

Summarizing the previous section:

ψ = { ψ 1 , if  x < − L / 2  (the region outside the box) ψ 2 , if  − L / 2 < x < L / 2  (the region inside the box) ψ 3 if  x > L / 2  (the region outside the box)

where we found ψ 1 , ψ 2 and ψ 3 to be:

ψ 1 = F e − α x + G e α x ψ 2 = A sin ⁡ ( k x ) + B cos ⁡ ( k x ) ψ 3 = H e − α x + I e α x

We see that as x goes to − ∞ , the F term goes to infinity. Likewise, as x goes to + ∞ , the I term goes to infinity. As the wave function must have finite total integral, this means we must set F = I = 0 , and we have:

Next, we know that the overall ψ function must be continuous and differentiable. In other words, the values of the functions and their derivatives must match up at the dividing points:

These equations have two sorts of solutions, symmetric, for which A = 0 and G = H , and antisymmetric, for which B = 0 and G = − H . For the symmetric case we get

H e − α L / 2 = B cos ⁡ ( k L / 2 ) − α H e − α L / 2 = − k B sin ⁡ ( k L / 2 )

so taking the ratio gives

α = k tan ⁡ ( k L / 2 ) .

Similarly for the antisymmetric case we get

α = − k cot ⁡ ( k L / 2 ) .

Recall that both α and k depend on the energy. What we have found is that the continuity conditions cannot be satisfied for an arbitrary value of the energy. Only certain energy values, which are solutions to one or either of these two equations, are allowed. Hence we find, as always, the bound-state energies are quantized.

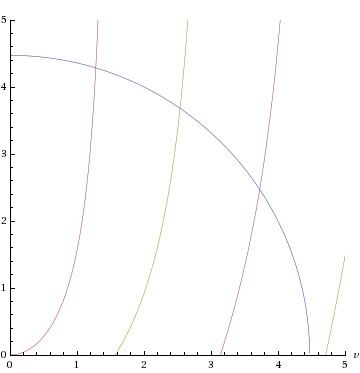
The energy equations cannot be solved analytically. Graphical or numerical solutions are aided by rewriting them a little. If we introduce the dimensionless variables u = α L / 2 and v = k L / 2 , and note from the definitions of α and k that u 2 = u 0 2 − v 2 , where u 0 2 = m L 2 V 0 / 2 ℏ 2 , the master equations read

u 0 2 − v 2 = { v tan ⁡ v , (symmetric case)  − v cot ⁡ v , (antisymmetric case) 

In the plot to the right, for u 0 2 = 20 , solutions exist where the blue semicircle intersects the purple or grey curves ( v tan ⁡ v and − v cot ⁡ v ). Each purple or grey curve represents a possible solution, v i within the range π 2 ( i − 1 ) ≤ v i < π 2 i . The total number of solutions, N , (i.e., the number of purple/grey curves that are intersected by the blue circle) is therefore determined by dividing the radius of the blue circle, u 0 , by the range of each solution π / 2 .

N = ⌊ 2 u 0 π ⌋ + 1 = ⌈ 2 u 0 π ⌉

In this case there are exactly three solutions, since N = ⌊ 2 20 / π ⌋ + 1 = ⌊ 2.85 ⌋ + 1 = 2 + 1 = 3 .

v 1 = 1.28 , v 2 = 2.54 and v 3 = 3.73 , with the corresponding energies

E n = 2 ℏ 2 v n 2 m L 2 .

If we want, we can go back and find the values of the constants A , B , G , H in the equations now (we also need to impose the normalisation condition). On the right we show the energy levels and wave functions in this case (where x 0 ≡ ℏ / 2 m V 0 ):

We note that however small u 0 is (however shallow or narrow the well), there is always at least one bound state.

Two special cases are worth noting. As the height of the potential becomes large, V 0 → ∞ , the radius of the semicircle gets larger and the roots get closer and closer to the values v n = n π / 2 , and we recover the case of the infinite square well.

The other case is that of a very narrow, deep well - specifically the case V 0 → ∞ and L → 0 with V 0 L fixed. As u 0 ∝ V 0 L 2 it will tend to zero, and so there will only be one bound state. The approximate solution is then v 2 = u 0 2 − u 0 4 , and the energy tends to E = − m L 2 V 0 2 / 2 ℏ 2 . But this is just the energy of the bound state of a Delta function potential of strength V 0 L , as it should be.

Note: The above derivation does not consider the possibility that the effective mass of the particle could be different inside the potential well and the region outside the well.

Spherical cavity

The results above can be used to show that, contrary to the one-dimensional case, there is not always a bound state in a spherical cavity.

The ground state of a spherically symmetric potential will always have zero orbital angular momentum, and the reduced wave function U ( r ) ≡ r ψ ( r ) satisfies the equation

− ℏ 2 2 m d 2 U d r 2 + V ( r ) U ( r ) = E U ( r )

This is identical to the one-dimensional equation, except for the boundary conditions. As before, U ( r ) and its first derivative must be continuous at the edge of the well r = R . However, there is another condition, that ψ ( 0 ) must be finite, and that requires U ( 0 ) = 0 .

By comparison with the solutions above, we can see that only the antisymmetric ones have nodes at the origin. Thus only the solutions to α = − k cot ⁡ ( k R ) are allowed. These correspond to the intersection of the semicircle with the grey curves, and so if the cavity is too shallow or small, there will be no bound state.