The Fibonacci word fractal is a fractal curve defined on the plane from the Fibonacci word.
This curve is built iteratively by applying, to the Fibonacci word 0100101001001...etc., the Odd–Even Drawing rule:
For each digit at position k :
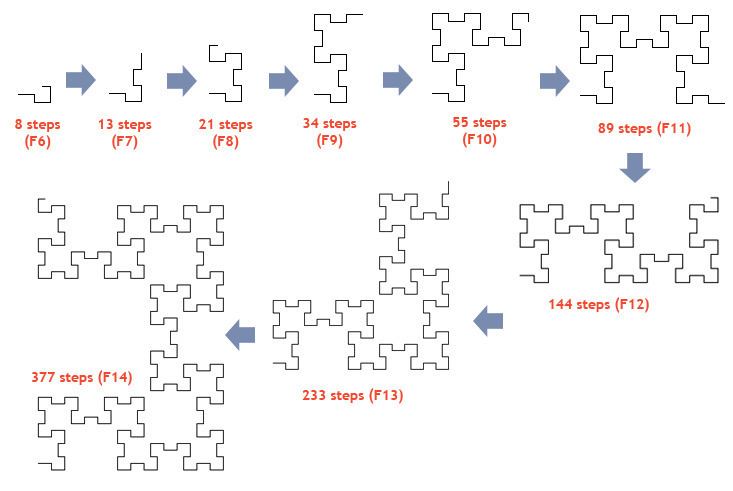
if the digit is 0 : draw a segment in the current directionif the digit is 1 : draw a segment after a 90° angle turn:to the right if k is evento the left if k is oddTo a Fibonacci word of length F n (the nth Fibonacci number) is associated a curve F n made of F n segments. The curve displays three different aspects whether n is in the form 3k, 3k + 1, or 3k + 2.
The curve F n , contains F n segments, F n − 1 right angles and F n − 2 flat angles.The curve never self-intersects and does not contain double points. At the limit, it contains an infinity of points asymptotically close.The curve presents self-similarities at all scales. The reduction ratio is 1 + 2 . This number, also called the silver ratio is present in a great number of properties listed below.The number of self-similarities at level n is a Fibonacci number \ −1. (more precisely : F 3 n + 3 − 1 ).The curve encloses an infinity of square structures of decreasing sizes in a ratio 1 + 2 . (see figure) The number of those square structures is a Fibonacci number.The curve F n can also be constructed by different ways (see gallery below):Iterated function system of 4 and 1 homothety of ratio 1 / ( 1 + 2 ) and 1 / ( 1 + 2 ) 2 By joining together the curves F n − 1 and F n − 2 Lindermayer systemBy an iterated construction of 8 square patterns around each square pattern.By an iterated construction of octagonsThe Hausdorff dimension of the Fibonacci word fractal is 3 log φ log ( 1 + 2 ) = 1 , 6379 , with φ = 1 + 5 2 , the golden ratio.Generalizing to an angle α between 0 and π / 2 , its Hausdorff dimension is 3 log φ log ( 1 + a + ( 1 + a ) 2 + 1 ) , with a = cos α .The Hausdorff dimension of its frontier is log 3 log ( 1 + 2 ) = 1 , 2465 .Exchanging the roles of "0" and "1" in the Fibonacci word, or in the drawing rule yields a similar curve, but oriented 45°.From the Fibonacci word, one can define the « dense Fibonacci word», on an alphabet of 3 letters : 102210221102110211022102211021102110221022102211021... ((sequence A143667 in the OEIS)). The usage, on this word, of a more simple drawing rule, defines an infinite set of variants of the curve, among which :a «diagonal varaint»a «svastika variant»a «compact variant »It is conjectured that the Fibonacci word fractal appears for every sturmian word for which the slope, written in continued fraction expansion, ends with an infinite series of "1".The juxtaposition of four F 3 k curves allows the construction of a closed curve enclosing a surface whose area is not null. This curve is called a "Fibonacci Tile".
The Fibonacci tile almost tiles the plane. The juxtaposition of 4 tiles (see illustration) leaves at the center a free square whose area tends to zero as k tends to infinity. At the limit, the infinite Fibonacci tile tiles the plane.If the tile is enclosed un a square of side 1, then its area tends to 2 − 2 = 0.5857 .The Fibonacci snowflake is a Fibonacci tile defined by:
q n = q n − 1 q n − 2 if n ≡ 2 ( mod 3 ) q n = q n − 1 q ¯ n − 2 otherwise.with q 0 = ϵ and q 1 = R , L = "turn left" et R = "turn right", and R ¯ = L ,
Several remarquable properties : · :
It is the Fibonacci tile associated to the "diagonal variant" previously defined.It tiles the plane at any order.It tiles the plane by translation in two different ways.its perimeter, at order n, equals 4 F ( 3 n + 1 ) . F ( n ) is the nth Fibonacci number.its area, at order n, follows the successive indexes of odd row of the Pell sequence (defined by P ( n ) = 2 P ( n − 1 ) + P ( n − 2 ) ).