 | ||
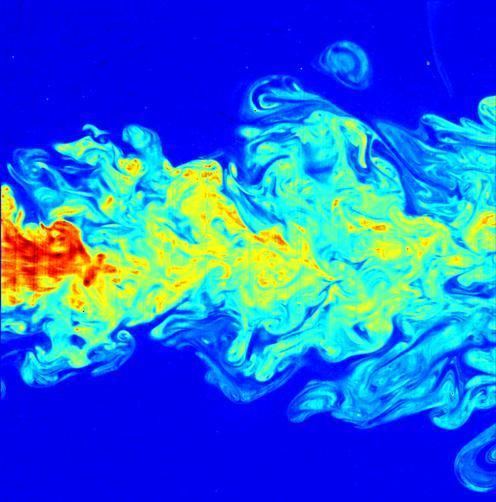
In continuum mechanics, an energy cascade refers to the transfer of energy from large scales of motion to the small scales – called a direct energy cascade. Or a transfer of energy from the small scales to the large scales – called an inverse energy cascade. This transfer of energy between different scales requires that the dynamics of the system is nonlinear.
Contents
- Spectra in the inertial subrange of turbulent flow
- Energy spectrum of turbulence
- Energy spectrum in the inertial subrange
- Spectrum of pressure fluctuations
- Spectrum of capillary disturbances at a free liquid surface
- References
This concept plays an important role in the study of well-developed turbulence. It was first expressed by Lewis F. Richardson in the 1920s. Also for wind waves, in the theory of wave turbulence, energy cascades are important.
Consider for instance turbulence generated by the air flow around a tall building: the energy-containing eddies generated by flow separation have sizes of the order of tens of meters. On the other side, dissipation by viscosity takes mainly place for eddies at the Kolmogorov microscales: this will be of the order of a millimetre for the present case. At the intermediate scales, there is neither a direct forcing of the flow nor a significant amount of viscous dissipation, but there is a net nonlinear transfer of energy from the large scales to the small scales.
This intermediate range of scales, if present, is called the inertial subrange. The dynamics at these scales is described by use of self-similarity, or by assumptions – for turbulence closure – on the statistical properties of the flow in the inertial subrange. Pioneering was the deduction by Andrey Kolmogorov, in the 1940s, of his model for the wavenumber spectrum in the turbulence inertial subrange.
Spectra in the inertial subrange of turbulent flow
The largest motions, or eddies, of turbulence contain most of the kinetic energy, whereas the smallest eddies are responsible for the viscous dissipation of turbulence kinetic energy. Kolmogorov hypothesized that when these scales are well separated, the intermediate range of length scales would be statistically isotropic and that its characteristics would depend only on the rate at which kinetic energy is dissipated.
Dissipation is the frictional conversion of mechanical energy to thermal energy. The dissipation rate, ε, may be written down in terms of the fluctuating rates of strain in the turbulent flow and the fluid's kinematic viscosity, ν. It has dimensions of energy per unit mass per second. The production of turbulent kinetic energy at the large scales of motion is accompanied by the dissipation of this energy at the small scales.
Energy spectrum of turbulence
The energy spectrum of turbulence, E(k), is related to the mean turbulence kinetic energy per unit mass as
where ui are the components of the fluctuating velocity, the overbar denotes an ensemble average, summation over i is implied, and k is the wavenumber. The energy spectrum, E(k), thus represents the contribution to turbulence kinetic energy by wavenumbers from k to k+dk. The largest eddies have low wavenumber, and the small eddies have high wavenumbers.
The dissipation rate may also be written in terms of the energy spectrum as:
with ν the kinematic viscosity of the fluid. From this equation, it may again be observed that dissipation is mainly associated with high wavenumbers (small eddies) whereas kinetic energy is associated mainly with lower wavenumbers (large eddies).
Energy spectrum in the inertial subrange
The transfer of energy from the low wavenumbers to the high wavenumbers is the energy cascade. This transfer brings turbulence kinetic energy from the large scales to the small scales, at which viscous friction dissipates it. In the intermediate range of scales, the so-called inertial subrange, Kolomogorov's hypotheses led to the following universal form for the energy spectrum:
An extensive body of experimental evidence supports this result, over a vast range of conditions. Experimentally, the value C = 1.5 is observed.
Spectrum of pressure fluctuations
The pressure fluctuations in a turbulent flow may be similarly characterized. The mean-square pressure fluctuation in a turbulent flow may be represented by a pressure spectrum, π(k):
For the case of turbulence with no mean velocity gradient (isotropic turbulence), the spectrum in the inertial subrange is given by
where ρ is the fluid density, and α = 1.32 C2 = 2.97. A mean-flow velocity gradient (shear flow) creates an additional, additive contribution to the inertial subrange pressure spectrum which varies as k−11/3; but the k−7/3 behavior is dominant at higher wavenumbers.
Spectrum of capillary disturbances at a free liquid surface
Turbulent pressure fluctuations below the free surface of a liquid can drive fluctuating displacements of the liquid surface. This free-surface-turbulence interaction may also be characterized by a wavenumber spectrum. If δ is the instantaneous displacement of the surface from its average position, the mean squared displacement may be represented with a displacement spectrum G(k) as:
A three dimensional form of the pressure spectrum may be combined with the Young-Laplace equation to show that:
Experimental observation of this k−19/3 law has been obtained by optical measurements of the surface of turbulent free liquid jets.
