Trisha Shetty (Editor)

Dimension (graph theory)

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Dimension (graph theory)

In mathematics, and particularly in graph theory, the dimension of a graph is the least integer n such that there exists a "classical representation" of the graph in the Euclidean space of dimension n with all the edges having unit length.

Contents

In a classical representation, the vertices must be distinct points, but the edges may cross one another.

The dimension of a graph G is written: dim ⁡ G .

For example, the Petersen graph can be drawn with unit edges in E 2 , but not in E 1 : its dimension is therefore 2 (see the figure to the right).

This concept was introduced in 1965 by Paul Erdős, Frank Harary and William Tutte. It generalises the concept of unit distance graph to more than 2 dimensions.

Complete graph

In the worst case, every pair of vertices is connected, giving a complete graph.

To immerse the complete graph K n with all the edges having unit length, we need the Euclidean space of dimension n − 1 . For example, it takes two dimensions to immerse K 3 (an equilateral triangle), and three to immerse K 4 (a regular tetrahedron) as shown to the right.

dim ⁡ K n = n − 1

In other words, the dimension of the complete graph is the same as that of the simplex having the same number of vertices.

Complete bipartite graphs

All star graphs K m , 1 , for m ≥ 3 , have dimension 2, as shown in the figure to the left. Star graphs with m equal to 1 or 2 need only dimension 1.

The dimension of a complete bipartite graph K m , 2 , for m ≥ 3 , can be drawn as in the figure to the right, by placing m vertices on a circle whose radius is less than a unit, and the other two vertices one each side of the plane of the circle, at a suitable distance from it. K 2 , 2 has dimension 2, as it can be drawn as a unit rhombus in the plane.

To summarise:

dim ⁡ K m , n = 1 , 2 , 3  or  4 , depending on the values of m and n.

Euclidean dimension

The definition of the dimension of a graph given above says, of the minimal-n representation:

  • if two vertices of G are connected by an edge, they must be at unit distance apart;
  • however, two vertices at unit distance apart are not necessarily connected by an edge.

    • This definition is rejected by some authors. A different definition was proposed in 1991 by Alexander Soifer, for what he termed the Euclidean dimension of a graph. Previously, in 1980, Paul Erdős and Miklós Simonovits had already proposed it with the name faithful dimension. By this definition, the minimal-n representation is one such that two vertices of the graph are connected if and only if their representations are at distance 1.

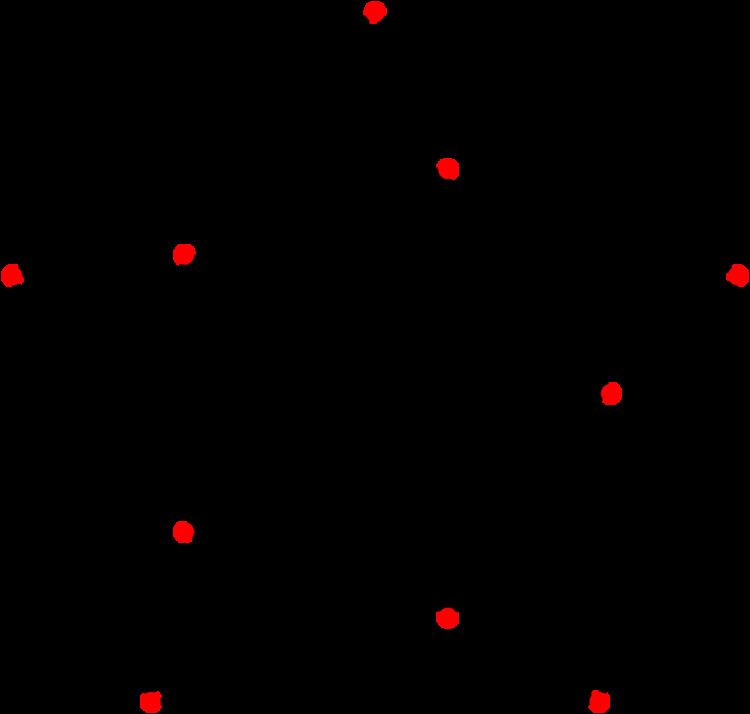
    The figures opposite show the difference between these definitions, in the case of a wheel graph having a central vertex and six peripheral vertices, with one spoke removed. Its representation in the plane allows two vertices at distance 1, but they are not connected.

    We write this dimension as Edim ⁡ G . It is never less than the dimension defined as above:

    dim ⁡ G ≤ Edim ⁡ G

    Euclidean dimension and maximal degree

    Paul Erdős and Miklós Simonovits proved the following result in 1980:

    Computational complexity

    It is NP-hard, and more specifically complete for the existential theory of the reals, to test whether the dimension or the Euclidean dimension of a given graph is at most a given value. The problem remains hard even for testing whether the dimension or Euclidean dimension is two.

    References

    Dimension (graph theory) Wikipedia
    (Text) CC BY-SA