 | ||
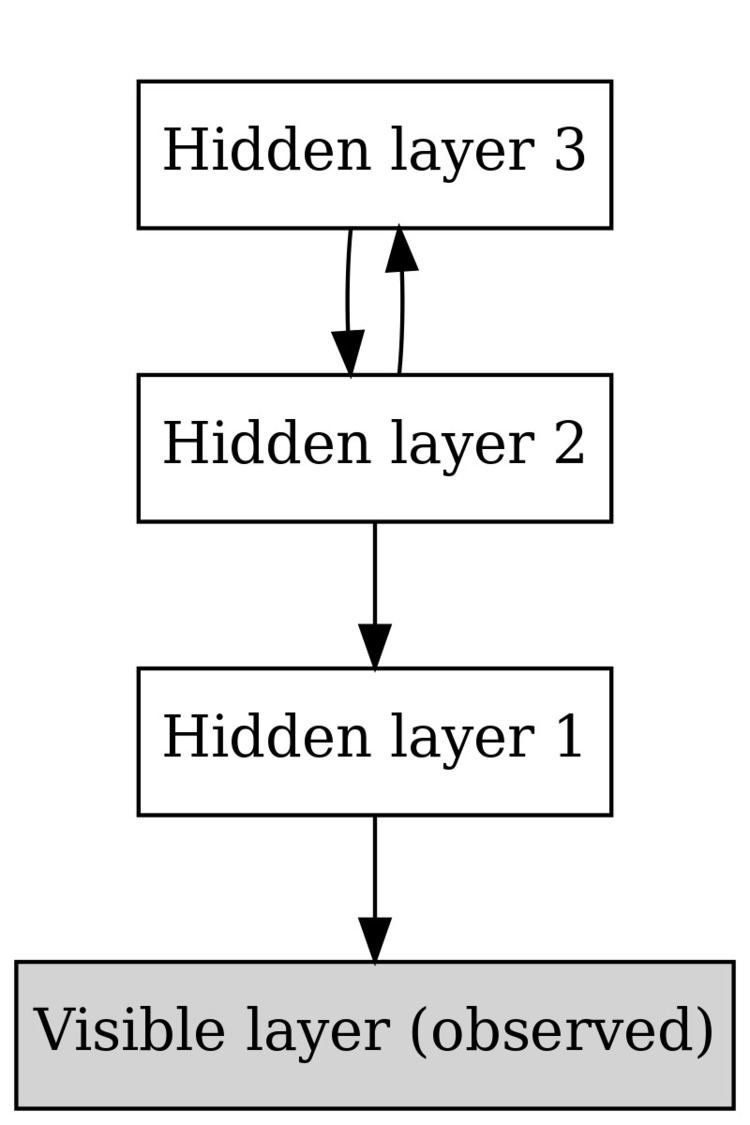
In machine learning, a deep belief network (DBN) is a generative graphical model, or alternatively a type of deep neural network, composed of multiple layers of latent variables ("hidden units"), with connections between the layers but not between units within each layer.
When trained on a set of examples in an unsupervised way, a DBN can learn to probabilistically reconstruct its inputs. The layers then act as feature detectors on inputs. After this learning step, a DBN can be further trained in a supervised way to perform classification.
DBNs can be viewed as a composition of simple, unsupervised networks such as restricted Boltzmann machines (RBMs) or autoencoders, where each sub-network's hidden layer serves as the visible layer for the next. This also leads to a fast, layer-by-layer unsupervised training procedure, where contrastive divergence is applied to each sub-network in turn, starting from the "lowest" pair of layers (the lowest visible layer being a training set).
The observation, due to Yee-Whye Teh, that DBNs can be trained greedily, one layer at a time, led to one of the first effective deep learning algorithms.
Training algorithm
The training algorithm for DBNs proceeds as follows. Let X be a matrix of inputs, regarded as a set of feature vectors.
- Train a restricted Boltzmann machine on X to obtain its weight matrix, W. Use this as the weight matrix between the lower two layers of the network.
- Transform X by the RBM to produce new data X', either by sampling or by computing the mean activation of the hidden units.
- Repeat this procedure with X ← X' for the next pair of layers, until the top two layers of the network are reached.
- Fine-tune all the parameters of this deep architecture with respect to a proxy for the DBN log- likelihood, or with respect to a supervised training criterion (after adding extra learning machinery to convert the learned representation into supervised predictions, e.g. a linear classifier).
