Cox–Ingersoll–Ross model - Alchetron, the free social encyclopedia

In mathematical finance, the Cox–Ingersoll–Ross model (or CIR model) describes the evolution of interest rates. It is a type of "one factor model" (short rate model) as it describes interest rate movements as driven by only one source of market risk. The model can be used in the valuation of interest rate derivatives. It was introduced in 1985 by John C. Cox, Jonathan E. Ingersoll and Stephen A. Ross as an extension of the Vasicek model.

The model

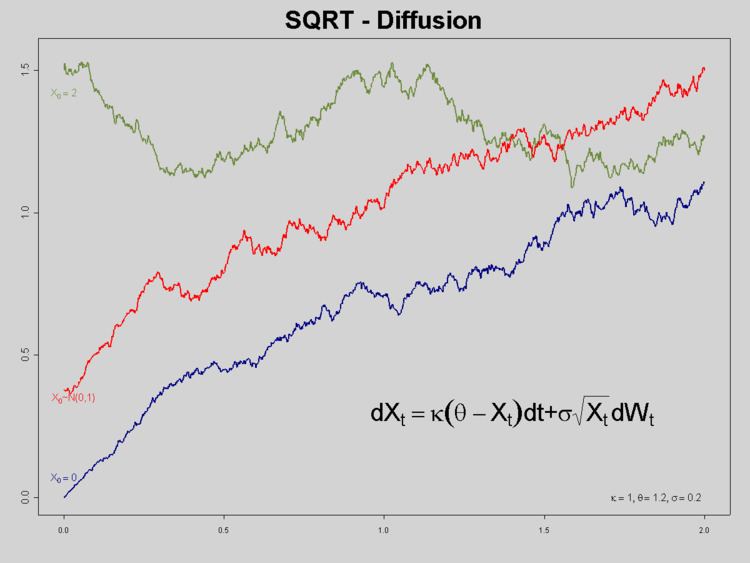
The CIR model specifies that the instantaneous interest rate follows the stochastic differential equation, also named the CIR Process:

d r t = a ( b − r t ) d t + σ r t d W t

where W t is a Wiener process (modelling the random market risk factor) and a , b , and σ are the parameters. The parameter a corresponds to the speed of adjustment, b to the mean and σ to volatility. The drift factor, a ( b − r t ) , is exactly the same as in the Vasicek model. It ensures mean reversion of the interest rate towards the long run value b , with speed of adjustment governed by the strictly positive parameter a .

The standard deviation factor, σ r t , avoids the possibility of negative interest rates for all positive values of a and b . An interest rate of zero is also precluded if the condition

2 a b ≥ σ 2

is met. More generally, when the rate ( r t ) is close to zero, the standard deviation ( σ r t ) also becomes very small, which dampens the effect of the random shock on the rate. Consequently, when the rate gets close to zero, its evolution becomes dominated by the drift factor, which pushes the rate upwards (towards equilibrium).

This process can be defined as a sum of squared Ornstein–Uhlenbeck process. The CIR is an ergodic process, and possesses a stationary distribution. The same process is used in the Heston model to model stochastic volatility.

Distribution

Future distribution

The distribution of future values of a CIR process can be computed in closed form:

r t + T = Y 2 c ,

where c = 2 a ( 1 − e − a T ) σ 2 , and Y is a non-central Chi-Squared distribution with 4 a b σ 2 degrees of freedom and non-centrality parameter 2 c r t e − a T . Formally the probability density function is:

f ( r t + T ; r t , a , b , σ ) = c e − u − v ( v u ) q / 2 I q ( 2 u v ) ,

where q = 2 a b σ 2 − 1 , u = c r t e − a T , v = c r t + T , and I q ( 2 u v ) is modified Bessel function of the first kind of order q .

Asymptotic distribution

Due to mean reversion, as time becomes large, the distribution of r ∞ will approach a gamma distribution with the probability density of:

f ( r ∞ ; a , b , σ ) = ω ν Γ ( ν ) r ∞ ν − 1 e − ω r ∞ ,

where ω = 2 a / σ 2 and ν = 2 a b / σ 2 .

Properties

Mean reversion,

Level dependent volatility ( σ r t ),

For given positive r 0 the process will never touch zero, if 2 a b ≥ σ 2 ; otherwise it can occasionally touch the zero point,

E [ r t | r 0 ] = r 0 e − a t + b ( 1 − e − a t ) , so long term mean is b ,

V a r [ r t | r 0 ] = r 0 σ 2 a ( e − a t − e − 2 a t ) + b σ 2 2 a ( 1 − e − a t ) 2 .

Calibration

Ordinary least squares

The continuous SDE can be discretized as follows

r t + Δ t − r t = a ( b − r t ) Δ t + σ r t Δ t ϵ t ,

which is equivalent to

r t + Δ t − r t r t = a b Δ t r t − a r t Δ t + σ Δ t ϵ t , provided ϵ t is n.i.i.d. (0,1). This equation can be used for a linear regression.

Martingale estimation

Maximum likelihood

Simulation

Stochastic simulation of the CIR process can be achieved using two variants:

Discretization

Exact

Bond pricing

Under the no-arbitrage assumption, a bond may be priced using this interest rate process. The bond price is exponential affine in the interest rate:

P ( t , T ) = A ( t , T ) exp ⁡ ( − B ( t , T ) r t )

where

A ( t , T ) = ( 2 h exp ⁡ ( ( a + h ) ( T − t ) / 2 ) 2 h + ( a + h ) ( exp ⁡ ( ( T − t ) h ) − 1 ) ) 2 a b / σ 2 B ( t , T ) = 2 ( exp ⁡ ( ( T − t ) h ) − 1 ) 2 h + ( a + h ) ( exp ⁡ ( ( T − t ) h ) − 1 ) h = a 2 + 2 σ 2

Extensions

Time varying functions replacing coefficients can be introduced in the model in order to make it consistent with a pre-assigned term structure of interest rates and possibly volatilities. The most general approach is in Maghsoodi (1996). A more tractable approach is in Brigo and Mercurio (2001b) where an external time-dependent shift is added to the model for consistency with an input term structure of rates. A significant extension of the CIR model to the case of stochastic mean and stochastic volatility is given by Lin Chen (1996) and is known as Chen model. A CIR process is a special case of a basic affine jump diffusion, which still permits a closed-form expression for bond prices.

References

Cox–Ingersoll–Ross model Wikipedia

(Text) CC BY-SA

Contents