Conceptual clustering

Conceptual clustering vs. data clustering

Conceptual clustering is obviously closely related to data clustering; however, in conceptual clustering it is not only the inherent structure of the data that drives cluster formation, but also the Description language which is available to the learner. Thus, a statistically strong grouping in the data may fail to be extracted by the learner if the prevailing concept description language is incapable of describing that particular regularity. In most implementations, the description language has been limited to feature conjunction, although in COBWEB (see "COBWEB" below), the feature language is probabilistic.

List of published algorithms

A fair number of algorithms have been proposed for conceptual clustering. Some examples are given below:

More general discussions and reviews of conceptual clustering can be found in the following publications:

Example: A basic conceptual clustering algorithm

This section discusses the rudiments of the conceptual clustering algorithm COBWEB. There are many other algorithms using different heuristics and "category goodness" or category evaluation criteria, but COBWEB is one of the best known. The reader is referred to the bibliography for other methods.

Knowledge representation

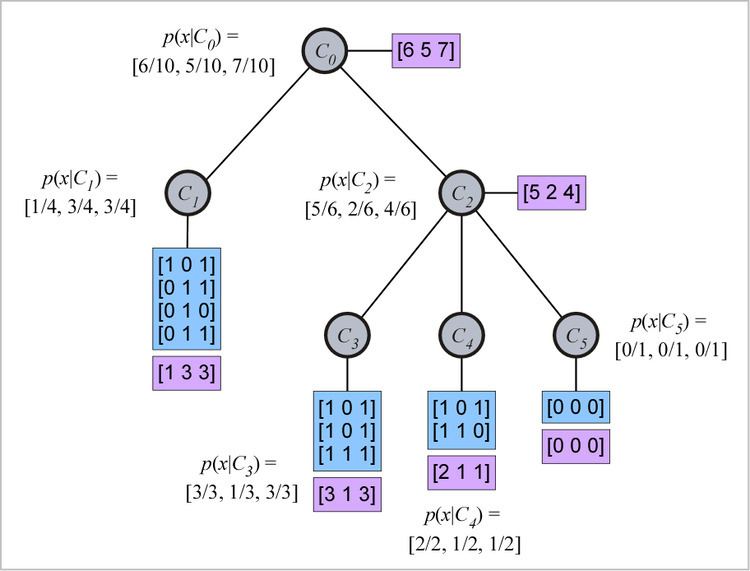
The COBWEB data structure is a hierarchy (tree) wherein each node represents a given concept. Each concept represents a set (actually, a multiset or bag) of objects, each object being represented as a binary-valued property list. The data associated with each tree node (i.e., concept) are the integer property counts for the objects in that concept. For example, (see figure), let a concept C 1 contain the following four objects (repeated objects being permitted).

1. [1 0 1]
2. [0 1 1]
3. [0 1 0]
4. [0 1 1]

The three properties might be, for example, [is_male, has_wings, is_nocturnal]. Then what is stored at this concept node is the property count [1 3 3], indicating that 1 of the objects in the concept is male, 3 of the objects have wings, and 3 of the objects are nocturnal. The concept description is the category-conditional probability (likelihood) of the properties at the node. Thus, given that an object is a member of category (concept) C 1 , the likelihood that it is male is 1 / 4 = 0.25 . Likewise, the likelihood that the object has wings and likelihood that the object is nocturnal or both is 3 / 4 = 0.75 . The concept description can therefore simply be given as [.25 .75 .75], which corresponds to the C 1 -conditional feature likelihood, i.e., p ( x | C 1 ) = ( 0.25 , 0.75 , 0.75 ) .

The figure to the right shows a concept tree with five concepts. C 0 is the root concept, which contains all ten objects in the data set. Concepts C 1 and C 2 are the children of C 0 , the former containing four objects, and the later containing six objects. Concept C 2 is also the parent of concepts C 3 , C 4 , and C 5 , which contain three, two, and one object, respectively. Note that each parent node (relative superordinate concept) contains all the objects contained by its child nodes (relative subordinate concepts). In Fisher's (1987) description of COBWEB, he indicates that only the total attribute counts (not conditional probabilities, and not object lists) are stored at the nodes. Any probabilities are computed from the attribute counts as needed.

The COBWEB language

The description language of COBWEB is a "language" only in a loose sense, because being fully probabilistic it is capable of describing any concept. However, if constraints are placed on the probability ranges which concepts may represent, then a stronger language is obtained. For example, we might permit only concepts wherein at least one probability differs from 0.5 by more than α . Under this constraint, with α = 0.3 , a concept such as [.6 .5 .7] could not be constructed by the learner; however a concept such as [.6 .5 .9] would be accessible because at least one probability differs from 0.5 by more than α . Thus, under constraints such as these, we obtain something like a traditional concept language. In the limiting case where α = 0.5 for every feature, and thus every probability in a concept must be 0 or 1, the result is a feature language base on conjunction; that is, every concept that can be represented can then be described as a conjunction of features (and their negations), and concepts that cannot be described in this way cannot be represented.

Evaluation criterion

In Fisher's (1987) description of COBWEB, the measure he uses to evaluate the quality of the hierarchy is Gluck and Corter's (1985) category utility (CU) measure, which he re-derives in his paper. The motivation for the measure is highly similar to the "information gain" measure introduced by Quinlan for decision tree learning. It has previously been shown that the CU for feature-based classification is the same as the mutual information between the feature variables and the class variable (Gluck & Corter, 1985; Corter & Gluck, 1992), and since this measure is much better known, we proceed here with mutual information as the measure of category "goodness".

What we wish to evaluate is the overall utility of grouping the objects into a particular hierarchical categorization structure. Given a set of possible classification structures, we need to determine whether one is better than another.