Chow–Liu tree

The Chow–Liu representation

The Chow–Liu method describes a joint probability distribution P ( X 1 , X 2 , … , X n ) as a product of second-order conditional and marginal distributions. For example, the six-dimensional distribution P ( X 1 , X 2 , X 3 , X 4 , X 5 , X 6 ) might be approximated as

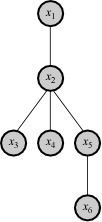
where each new term in the product introduces just one new variable, and the product can be represented as a first-order dependency tree, as shown in the figure. The Chow–Liu algorithm (below) determines which conditional probabilities are to be used in the product approximation. In general, unless there are no third-order or higher-order interactions, the Chow–Liu approximation is indeed an approximation, and cannot capture the complete structure of the original distribution. Pearl (1988) provides a modern analysis of the Chow–Liu tree as a Bayesian network.

The Chow–Liu algorithm

Chow and Liu show how to select second-order terms for the product approximation so that, among all such second-order approximations (first-order dependency trees), the constructed approximation P ′ has the minimum Kullback–Leibler distance to the actual distribution P , and is thus the closest approximation in the classical information-theoretic sense. The Kullback–Leibler distance between a second-order product approximation and the actual distribution is shown to be

where I ( X i ; X j ( i ) ) is the mutual information between variable X i and its parent X j ( i ) and H ( X 1 , X 2 , … , X n ) is the joint entropy of variable set { X 1 , X 2 , … , X n } . Since the terms ∑ H ( X i ) and H ( X 1 , X 2 , … , X n ) are independent of the dependency ordering in the tree, only the sum of the pairwise mutual informations, ∑ I ( X i ; X j ( i ) ) , determines the quality of the approximation. Thus, if every branch (edge) on the tree is given a weight corresponding to the mutual information between the variables at its vertices, then the tree which provides the optimal second-order approximation to the target distribution is just the maximum-weight tree. The equation above also highlights the role of the dependencies in the approximation: When no dependencies exist, and the first term in the equation is absent, we have only an approximation based on first-order marginals, and the distance between the approximation and the true distribution is due to the redundancies that are not accounted for when the variables are treated as independent. As we specify second-order dependencies, we begin to capture some of that structure and reduce the distance between the two distributions.

Chow and Liu provide a simple algorithm for constructing the optimal tree; at each stage of the procedure the algorithm simply adds the maximum mutual information pair to the tree. See the original paper, Chow & Liu (1968), for full details. A more efficient tree construction algorithm for the common case of sparse data was outlined in Meilă (1999).

Chow and Wagner proved in a later paper Chow & Wagner (1973) that the learning of the Chow–Liu tree is consistent given samples (or observations) drawn i.i.d. from a tree-structured distribution. In other words, the probability of learning an incorrect tree decays to zero as the number of samples tends to infinity. The main idea in the proof is the continuity of the mutual information in the pairwise marginal distribution. Recently, the exponential rate of convergence of the error probability was provided.

Variations on Chow–Liu trees

The obvious problem which occurs when the actual distribution is not in fact a second-order dependency tree can still in some cases be addressed by fusing or aggregating together densely connected subsets of variables to obtain a "large-node" Chow–Liu tree (Huang & King 2002), or by extending the idea of greedy maximum branch weight selection to non-tree (multiple parent) structures (Williamson 2000). (Similar techniques of variable substitution and construction are common in the Bayes network literature, e.g., for dealing with loops. See Pearl (1988).)

Generalizations of the Chow–Liu tree are the so-called t-cherry junction trees. It is proved that the t-cherry junction trees provide a better or at least as good approximation for a discrete multivariate probability distribution as the Chow–Liu tree gives. For the third order t-cherry junction tree see (Kovács & Szántai 2010), for the kth-order t-cherry junction tree see (Szántai & Kovács 2010). The second order t-cherry junction tree is in fact the Chow–Liu tree.