Bonaventura Cavalieri

Life

Born in Milan, Cavalieri joined the Jesuites order (not to be confused with the Jesuits) at the age of fifteen and remained a member until his death. He studied theology in the monastery of San Gerolamo in Milan, and geometry at the University of Pisa.

He published eleven books, his first being published in 1632. He worked on the problems of optics and motion. His astronomical and astrological work remained marginal to these main interests, though his last book, Trattato della ruota planetaria perpetua (1646), was dedicated to the former.

He was introduced to Galileo Galilei through academic and ecclesiastical contacts. Galileo exerted a strong influence on Cavalieri encouraging him to work on his new method and suggesting fruitful ideas, and Cavalieri would write at least 112 letters to Galileo. Galileo said of Cavalieri, "few, if any, since Archimedes, have delved as far and as deep into the science of geometry." He also benefited from the patronage of Cesare Marsili.

Cavalieri's first book was Lo Specchio Ustorio, overo, Trattato delle settioni coniche, or The Burning Mirror, or a Treatise on Conic Sections. In this book he developed the theory of mirrors shaped into parabolas, hyperbolas, and ellipses, and various combinations of these mirrors. The work was purely theoretical since the needed mirrors could not be constructed with the technologies of the time, a limitation well understood by Cavalieri.

Inspired by earlier work by Galileo, Cavalieri developed a new geometrical approach called the method of indivisibles to calculus and published a treatise on the topic, Geometria indivisibilibus continuorum nova quadam ratione promota (Geometry, developed by a new method through the indivisibles of the continua, 1635). In this work, an area is considered as constituted by an indefinite number of parallel segments and a volume as constituted by an indefinite number of parallel planar areas. Such elements are called indivisibles respectively of area and volume and provide the building blocks of Cavalieri's method. As an application, he computed the areas under the curves y = x n – an early integral – which is known as Cavalieri's quadrature formula.

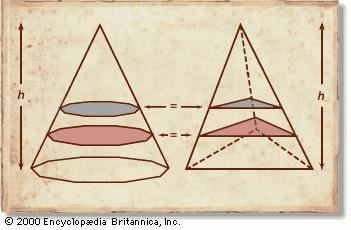
Cavalieri is known for Cavalieri's principle, which states that the volumes of two objects are equal if the areas of their corresponding cross-sections are in all cases equal. Two cross-sections correspond if they are intersections of the body with planes equidistant from a chosen base plane. (The same principle had been previously discovered by Zu Gengzhi (480–525) of China.) Cavalieri also constructed a hydraulic pump for his monastery and published tables of logarithms, emphasizing their practical use in the fields of astronomy and geography.

He died in Bologna.

Legacy

According to Gilles-Gaston Granger, Cavalieri belongs with Newton, Leibniz, Pascal, Wallis and MacLaurin as one of those who in the 17th and 18th centuries "redefine[d] the mathematical object".

The lunar crater Cavalerius is named for Cavalieri.