Bolzano–Weierstrass theorem

Proof

First we prove the theorem when n = 1 , in which case the ordering on R can be put to good use. Indeed, we have the following result.

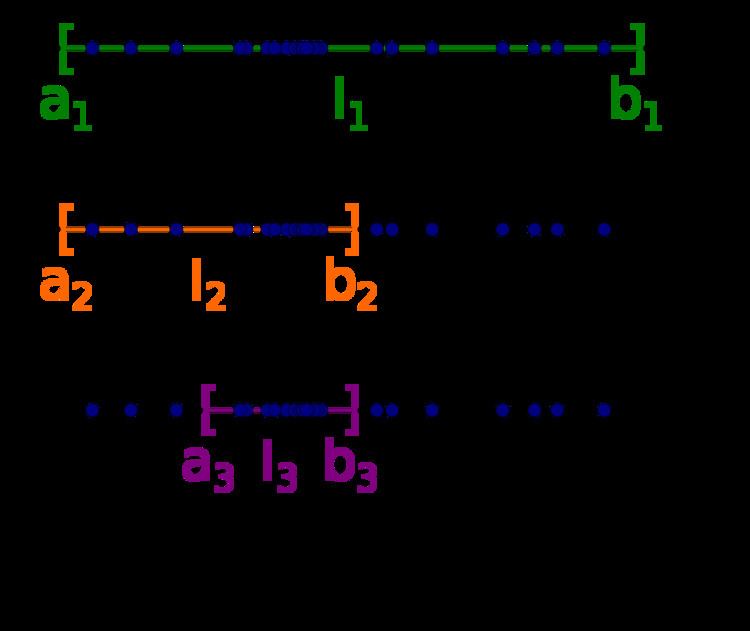
Lemma: Every sequence ( x n ) in R has a monotone subsequence.

Proof: Let us call a positive integer n a "peak of the sequence" if n < m implies x n > x m i.e., if x n is greater than every subsequent term x m in the sequence. Suppose first that the sequence has infinitely many peaks, n 1 < n 2 < n 3 < ⋯ < n j < … . Then the subsequence ( x n j ) corresponding to these peaks is monotonically decreasing. So suppose now that there are only finitely many peaks, let N be the last peak and n 1 = N + 1 . Then n 1 is not a peak, since N < n 1 , which implies the existence of n 2 with n 1 < n 2 and x n 1 ≤ x n 2 . Again, n 2 > N is not a peak, hence there is an n 3 where n 2 < n 3 with x n 2 ≤ x n 3 . Repeating this process leads to an infinite non-decreasing subsequence  x n 1 ≤ x n 2 ≤ x n 3 ≤ … , as desired.

Now suppose one has a bounded sequence in R ; by the lemma there exists a monotone subsequence, necessarily bounded. It follows from the monotone convergence theorem that this subsequence must converge.

Finally, the general case can be reduced to the case of n = 1 as follows: given a bounded sequence in R n , the sequence of first coordinates is a bounded real sequence, hence has a convergent subsequence. One can then extract a subsubsequence on which the second coordinates converge, and so on, until in the end we have passed from the original sequence to a subsequence n times—which is still a subsequence of the original sequence—on which each coordinate sequence converges, hence the subsequence itself is convergent.

Alternative proof

There is also an alternative proof of the Bolzano–Weierstrass theorem using nested intervals. We start with a bounded sequence ( x n ) :

Because we halve the length of an interval at each step the limit of the interval's length is zero. Thus there is a number x which is in each Interval I n . Now we show, that x is an accumulation point of ( x n ) .

Take a neighbourhood U of x . Because the length of the intervals converges to zero, there is an Interval I N which is a subset of U . Because I N contains by construction infinitely many members of ( x n ) and I N ⊆ U , also U contains infinitely many members of ( x n ) . This proves, that x is an accumulation point of ( x n ) . Thus, there is a subsequence of ( x n ) which converges to x .

Sequential compactness in Euclidean spaces

Suppose A is a subset of Rⁿ with the property that every sequence in A has a subsequence converging to an element of A. Then A must be bounded, since otherwise there exists a sequence x_m in A with || x_m || ≥ m for all m, and then every subsequence is unbounded and therefore not convergent. Moreover, A must be closed, since from a noninterior point x in the complement of A one can build an A-valued sequence converging to x. Thus the subsets A of Rⁿ for which every sequence in A has a subsequence converging to an element of A – i.e., the subsets which are sequentially compact in the subspace topology – are precisely the closed and bounded sets.

This form of the theorem makes especially clear the analogy to the Heine–Borel theorem, which asserts that a subset of Rⁿ is compact if and only if it is closed and bounded. In fact, general topology tells us that a metrizable space is compact if and only if it is sequentially compact, so that the Bolzano–Weierstrass and Heine–Borel theorems are essentially the same.

History

The Bolzano–Weierstrass theorem is named after mathematicians Bernard Bolzano and Karl Weierstrass. It was actually first proved by Bolzano in 1817 as a lemma in the proof of the intermediate value theorem. Some fifty years later the result was identified as significant in its own right, and proved again by Weierstrass. It has since become an essential theorem of analysis.

Application to economics

There are different important equilibrium concepts in economics, the proofs of the existence of which often require variations of the Bolzano–Weierstrass theorem. One example is the existence of a Pareto efficient allocation. An allocation is a matrix of consumption bundles for agents in an economy, and an allocation is Pareto efficient if no change can be made to it which makes no agent worse off and at least one agent better off (here rows of the allocation matrix must be rankable by a preference relation). The Bolzano–Weierstrass theorem allows one to prove that if the set of allocations is compact and non-empty, then the system has a Pareto-efficient allocation.