Atan2

History and motivation

The atan2 function was first introduced in computer programming languages, but now it is also common in other fields of science and engineering. It dates back at least as far as the FORTRAN programming language and is currently found in many modern programming languages. Among these languages are: C's math.h standard library, the Java Math library, .NET's System.Math (usable from C#, VB.NET, etc.), the Python math module, the Ruby Math module, and elsewhere. In addition, many scripting languages, such as Perl, include the C-style atan2(y,x) function.

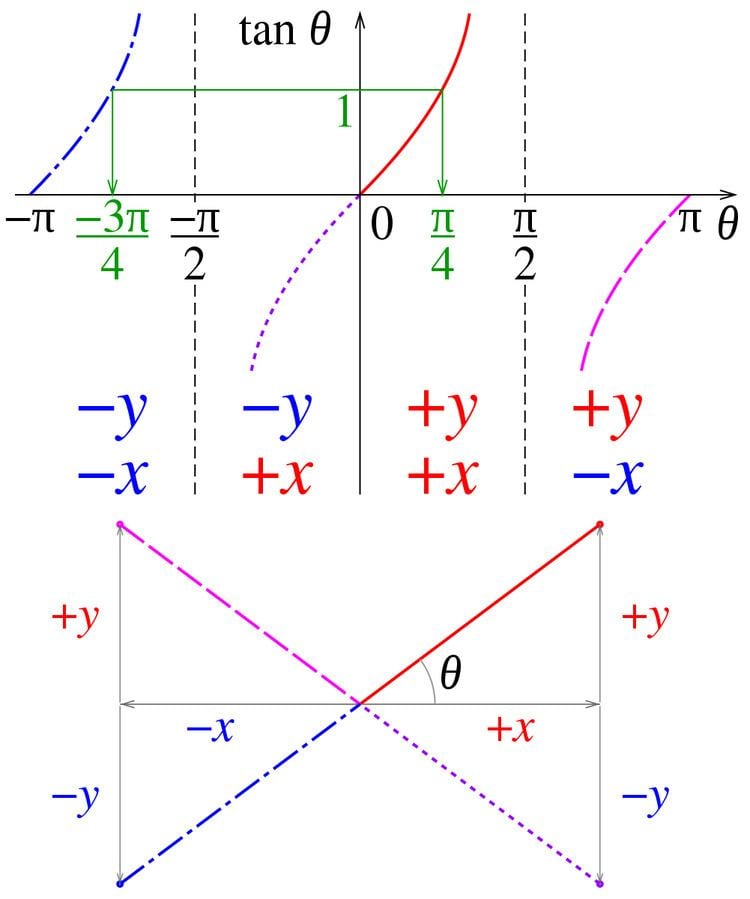
The one-argument arctangent function cannot distinguish between diametrically opposite directions. For example, the anticlockwise angle from the x-axis to the vector (1, 1), calculated in the usual way as arctan(1/1), is π/4 (radians), or 45°. However, the angle between the x-axis and the vector (−1, −1) appears, by the same method, to be arctan(−1/−1), again π/4, even though the answer clearly should be −3π/4, or −135°. In addition, an attempt to find the angle between the x-axis and the vector (0, 1) requires evaluation of arctan(1/0), which fails on division by zero.

The atan2 function calculates the arc tangent of the two variables y and x. It is similar to calculating the arc tangent of y/x, except that the signs of both arguments are used to determine the quadrant of the result. Thus, the atan2 function takes into account the signs of both vector components, and places the angle in the correct quadrant, e.g., atan2 (1, 1) = π/4 and atan2 (−1, −1) = −3π/4. In addition, atan2 can produce an angle of ±π/2 (or ±90°) while the ordinary arctangent method breaks down, e.g., atan2 (1, 0 )= π/2.

When calculations are performed manually, the necessary quadrant corrections and exception handling can be done by inspection, but it is extremely useful to have a single function that always gives an unambiguous correct result. The atan2 function is useful in many applications involving vectors in Euclidean space, such as finding the direction from one point to another. A principal use is in computer graphics rotations, for converting rotation matrix representations into Euler angles.

Definition and computation

The function atan2 computes the principal value of the argument function applied to the complex number x+iy. That is, atan2(y, x) = Pr arg(x+iy) = Arg(x+iy). The argument can be changed by 2π (corresponding to a complete turn around the origin) without making any difference to the angle, but to define atan2 uniquely one uses the principal value in the range (−π, π]. That is, −π < atan2(y, x) ≤ π.

In terms of the standard arctan function, whose range is (−π/2, π/2), it can be expressed as follows:

atan2 ⁡ ( y , x ) = { arctan ⁡ ( y x ) if  x > 0 , arctan ⁡ ( y x ) + π if  x < 0  and  y ≥ 0 , arctan ⁡ ( y x ) − π if  x < 0  and  y < 0 , + π 2 if  x = 0  and  y > 0 , − π 2 if  x = 0  and  y < 0 , undefined if  x = 0  and  y = 0.

A more compact expression with four overlapping half-planes is

atan2 ⁡ ( y , x ) = { arctan ⁡ ( y x ) if  x > 0 , π 2 − arctan ⁡ ( x y ) if  y > 0 , − π 2 − arctan ⁡ ( x y ) if  y < 0 , arctan ⁡ ( y x ) ± π if  x < 0 , undefined if  x = 0  and  y = 0.

The following expression derived from the tangent half-angle formula can also be used to define atan2:

atan2 ⁡ ( y , x ) = { 2 arctan ⁡ ( y x 2 + y 2 + x ) if  x > 0  or  y ≠ 0 , π if  x < 0  and  y = 0 , undefined if  x = 0  and  y = 0.

This expression may be more suited for symbolic use than the definition above. However it is unsuitable for floating point computational use, as the effect of rounding errors in x 2 + y 2 is blown up near the region x < 0, y = 0 (this may even lead to a division of y by zero).

A variant of the last formula which avoids rounding errors being blown up is sometimes used in high precision computation:

atan2 ⁡ ( y , x ) = { 2 arctan ⁡ ( y x 2 + y 2 + x ) if  x > 0 , 2 arctan ⁡ ( x 2 + y 2 − x y ) if  x ≤ 0  and  y ≠ 0 , π if  x < 0  and  y = 0 , undefined if  x = 0  and  y = 0.

Notes:

This produces results in the range (−π, π], which can be mapped to [0, 2π) by adding 2π to negative results.

As mentioned above, the principal value of the argument atan2(y, x) can be related to arctan(y/x) by trigonometry. The derivation goes as follows:

If (x,y) = (r cos θ, r sin θ) then tan θ/2 = y/r + x. It follows that

atan2 ( y , x ) = θ = 2 θ 2 = 2 arctan ⁡ y x 2 + y 2 + x   .

Note that √x² + y² + x ≠ 0 in the domain in question.

Derivative

As the function atan2 is a function of two variables, it has two partial derivatives. At points where these derivatives exist, atan2 is, except for a constant, equal to arctan(y/x). Hence for x > 0 or y ≠ 0,

∂ ∂ x atan2 ⁡ ( y , x ) = ∂ ∂ x arctan ⁡ ( y x ) = − y x 2 + y 2 , ∂ ∂ y atan2 ⁡ ( y , x ) = ∂ ∂ y arctan ⁡ ( y x ) = x x 2 + y 2 .

Thus the gradient of atan2 is given by

∇ atan2 ( y , x ) = ( x x 2 + y 2 ,   − y x 2 + y 2 ) .

Informally representing the function atan2 as the angle function θ(x, y) = atan2(y, x) (which is only defined up to a constant) yields the following formula for the total differential:

d θ = ∂ ∂ x atan2 ⁡ ( y , x ) d x + ∂ ∂ y atan2 ⁡ ( y , x ) d y = − y x 2 + y 2 d x + x x 2 + y 2 d y .

While the function atan2 is discontinuous along the negative y-axis, reflecting the fact that angle cannot be continuously defined, this derivative is continuously defined except at the origin, reflecting the fact that infinitesimal (and indeed local) changes in angle can be defined everywhere except the origin. Integrating this derivative along a path gives the total change in angle over the path, and integrating over a closed loop gives the winding number.

In the language of differential geometry, this derivative is a one-form, and it is closed (its derivative is zero) but not exact (it is not the derivative of a 0-form, i.e., a function), and in fact it generates the first de Rham cohomology of the punctured plane. This is the most basic example of such a form, and it is fundamental in differential geometry.

The partial derivatives of atan2 do not contain trigonometric functions, making it particularly useful in many applications (e.g. embedded systems) where trigonometric functions can be expensive to evaluate.

Illustrations

The figure alongside shows values of atan2 at selected points on the unit circle. The values, in radians, are shown inside the circle. The diagram uses the standard mathematical convention that angles increase counterclockwise, and zero is to the right. Note that the order of arguments is reversed; the function atan2(y, x) computes the angle corresponding to the point (x, y).

The figure below shows values of atan2 for points on the unit circle. On the x-axis is the angle of the points, starting from 0 (point (1, 0)) and going counterclockwise, through points:

(0, 1) with angle π/2 (in radians);

(−1, 0) with angle π;

(0, −1) with angle 3π/2;

to (1, 0) with angle 0 = (2πn mod 2π). One can clearly see the branch cut of the atan2 function.

The two figures below show 3D view of respectively atan2(y, x) and arctan(y/x) over a region of the plane. Note that for atan2(y, x), rays emanating from the origin have constant values, but for arctan(y/x) lines passing through the origin have constant values. For x > 0, the two diagrams give identical values.

Addition sum and difference identity

Sums of atan2 may be collapsed into a single operation according to the following identity

atan2 ⁡ ( y 1 , x 1 ) ± atan2 ⁡ ( y 2 , x 2 ) = atan2 ⁡ ( y 1 x 2 ± y 2 x 1 , x 1 x 2 ∓ y 1 y 2 )

...provided that atan2 ⁡ ( y 1 , x 1 ) ± atan2 ⁡ ( y 2 , x 2 ) ∈ ( − π , π ] .

The proof involves considering two cases, one where y 2 ≠ 0 or x 2 > 0 and one where y 2 = 0 and x 2 < 0 .

We only consider the case where y 2 ≠ 0 or x 2 > 0 . To start, we make the following observations:

1. − atan2 ⁡ ( y , x ) = atan2 ⁡ ( − y , x ) provided that y ≠ 0 or x > 0 .
2. Arg ⁡ ( x + i y ) = atan2 ⁡ ( y , x ) , where Arg is the complex argument function.
3. θ = Arg ⁡ e i θ whenever θ ∈ ( − π , π ] , a consequence of Euler's formula.
4. Arg ⁡ ( e i Arg ⁡ ζ 1 e i Arg ⁡ ζ 2 ) = Arg ⁡ ( ζ 1 ζ 2 ) .

To see (4), we have the identity e i Arg ⁡ ζ = ζ ¯ where ζ ¯ = ζ / | ζ | , hence Arg ⁡ ( e i Arg ⁡ ζ 1 e i Arg ⁡ ζ 2 ) = Arg ⁡ ( ζ 1 ¯ ζ 2 ¯ ) . Furthermore, since Arg ⁡ ζ = Arg ⁡ a ζ for any positive real value a , then if we let ζ = ζ 1 ζ 2 and a = | ζ 1 | | ζ 2 | then we have Arg ⁡ ( ζ 1 ¯ ζ 2 ¯ ) = Arg ⁡ ( ζ 1 ζ 2 ) .

From these observations have following equivalences:

atan2 ⁡ ( y 1 , x 1 ) ± atan2 ⁡ ( y 2 , x 2 ) = atan2 ⁡ ( y 1 , x 1 ) + atan2 ⁡ ( ± y 2 , x 2 ) by (1) = Arg ⁡ ( x 1 + i y 1 ) + Arg ⁡ ( x 2 ± i y 2 ) by (2) = Arg ⁡ e i ( Arg ⁡ ( x 1 + i y 1 ) + Arg ⁡ ( x 2 ± i y 2 ) ) by (3) = Arg ⁡ ( e i Arg ⁡ ( x 1 + i y 1 ) e i Arg ⁡ ( x 2 ± i y 2 ) ) ) = Arg ⁡ ( ( x 1 + i y 1 ) ( x 2 ± i y 2 ) ) by (4) = Arg ⁡ ( x 1 x 2 ∓ y 1 y 2 + i ( y 1 x 2 ± y 2 x 1 ) ) = atan2 ⁡ ( y 1 x 2 ± y 2 x 1 , x 1 x 2 ∓ y 1 y 2 ) by (2)

Realizations of the function in common computer languages

The realization of the function differs from one computer languages to another:

The C function atan2, and most other computer implementations, are designed to reduce the effort of transforming cartesian to polar coordinates and so always define atan2(0, 0). On implementations without signed zero, or when given positive zero arguments, it is normally defined as 0. It will always return a value in the range [−π, π] rather than raising an error or returning a NaN (Not a Number).

In Common Lisp, where optional arguments exist, the atan function allows one to optionally supply the x coordinate: (atan y x).

In Mathematica, the form ArcTan[x, y] is used where the one parameter form supplies the normal arctangent. Mathematica classifies ArcTan[0, 0] as an indeterminate expression.

In Microsoft Excel, OpenOffice.org Calc, LibreOffice Calc, Google Spreadsheets, iWork Numbers, and ANSI SQL:2008 standard, the atan2 function has the two arguments reversed.

In the Intel Architecture assembler code, atan2 is known as the FPATAN (floating-point partial arctangent) instruction. It can deal with infinities and results lie in the closed interval [−π, π], e.g. atan2(∞, x) = +π/2 for finite x. Particularly, FPATAN is defined when both arguments are zero:atan2(+0, +0) = +0;atan2(+0, −0) = +π;atan2(−0, +0) = −0;atan2(−0, −0) = −π.

This definition is related to the concept of signed zero.

On most TI graphing calculators (excluding the TI-85 and TI-86), the equivalent function is called R►Pθ and has the arguments reversed.

On TI-85 the arg function is called angle(x,y) and although it appears to take two arguments, it really only has one complex argument which is denoted by a pair of numbers: x + yi = (x, y).

In mathematical writings other than source code, such as in books and articles, the notations Arctan and Tan⁻¹ have been utilized; these are uppercase variants of the regular arctan and tan⁻¹. This usage is consistent with the complex argument notation, such that Atan(y, x) = Arg(x + yi).

On HP calculators, treat the coordinates as a complex number and then take the ARG. Or << C->R ARG >> 'ATAN2' STO.

On scientific calculators the function can often be calculated as the angle given when (x, y) is converted from rectangular coordinates to polar coordinates.

Systems supporting symbolic mathematics normally return an undefined value for atan2(0, 0) or otherwise signal that an abnormal condition has arisen.

For systems implementing signed zero, infinities, or Not a Number (for example, IEEE floating point), it is common to implement reasonable extensions which may extend the range of values produced to include −π and −0. These also may return NaN or raise an exception when given a NaN argument.

For systems implementing signed zero (for example, IEEE floating point), atan2(−0, x), x < 0 returns the value −π. atan2(+0, x), x < 0 still returns +π.

The free math library FDLIBM (Freely Distributable LIBM) available from netlib has source code showing how it implements atan2 including handling the various IEEE exceptional values.

For systems without a hardware multiplier the function atan2 can be implemented in a numerically reliable manner by the CORDIC method. Thus implementations of atan(y) will probably choose to compute atan2(y, 1).