Additive white Gaussian noise - Alchetron, the free social encyclopedia

Additive white Gaussian noise (AWGN) is a basic noise model used in Information theory to mimic the effect of many random processes that occur in nature. The modifiers denote specific characteristics:

Wideband noise comes from many natural sources, such as the thermal vibrations of atoms in conductors (referred to as thermal noise or Johnson-Nyquist noise), shot noise, black body radiation from the earth and other warm objects, and from celestial sources such as the Sun. The central limit theorem of probability theory indicates that the summation of many random processes will tend to have distribution called Gaussian or Normal.

AWGN is often used as a channel model in which the only impairment to communication is a linear addition of wideband or white noise with a constant spectral density (expressed as watts per hertz of bandwidth) and a Gaussian distribution of amplitude. The model does not account for fading, frequency selectivity, interference, nonlinearity or dispersion. However, it produces simple and tractable mathematical models which are useful for gaining insight into the underlying behavior of a system before these other phenomena are considered.

The AWGN channel is a good model for many satellite and deep space communication links. It is not a good model for most terrestrial links because of multipath, terrain blocking, interference, etc. However, for terrestrial path modeling, AWGN is commonly used to simulate background noise of the channel under study, in addition to multipath, terrain blocking, interference, ground clutter and self interference that modern radio systems encounter in terrestrial operation.

Channel capacity

The AWGN channel is represented by a series of outputs Y i at discrete time event index i . Y i is the sum of the input X i and noise, Z i , where Z i is independent and identically distributed and drawn from a zero-mean normal distribution with variance N (the noise). The Z i are further assumed to not be correlated with the X i .

Z i ∼ N ( 0 , N ) Y i = X i + Z i ∼ N ( X i , N ) .

The capacity of the channel is infinite unless the noise n is nonzero, and the X i are sufficiently constrained. The most common constraint on the input is the so-called "power" constraint, requiring that for a codeword ( x 1 , x 2 , … , x k ) transmitted through the channel, we have:

1 k ∑ i = 1 k x i 2 ≤ P ,

where P represents the maximum channel power. Therefore, the channel capacity for the power-constrained channel is given by:

C = max f ( x ) s.t. E ( X 2 ) ≤ P I ( X ; Y )

Where f ( x ) is the distribution of X . Expand I ( X ; Y ) , writing it in terms of the differential entropy:

I ( X ; Y ) = h ( Y ) − h ( Y | X ) = h ( Y ) − h ( X + Z | X ) = h ( Y ) − h ( Z | X )

But X and Z are independent, therefore:

I ( X ; Y ) = h ( Y ) − h ( Z )

Evaluating the differential entropy of a Gaussian gives:

h ( Z ) = 1 2 log ⁡ ( 2 π e N )

Because X and Z are independent and their sum gives Y :

E ( Y 2 ) = E ( X + Z ) 2 = E ( X 2 ) + 2 E ( X ) E ( Z ) + E ( Z 2 ) = P + N

From this bound, we infer from a property of the differential entropy that

h ( Y ) ≤ 1 2 log ⁡ ( 2 π e ( P + N ) )

Therefore, the channel capacity is given by the highest achievable bound on the mutual information:

I ( X ; Y ) ≤ 1 2 log ⁡ ( 2 π e ( P + N ) ) − 1 2 log ⁡ ( 2 π e N )

Where I ( X ; Y ) is maximized when:

X ∼ N ( 0 , P )

Thus the channel capacity C for the AWGN channel is given by:

C = 1 2 log ⁡ ( 1 + P N )

Channel capacity and sphere packing

Suppose that we are sending messages through the channel with index ranging from 1 to M , the number of distinct possible messages. If we encode the M messages to n bits, then we define the rate R as:

R = log ⁡ M n

A rate is said to be achievable if there is a sequence of codes so that the maximum probability of error tends to zero as n approaches infinity. The capacity C is the highest achievable rate.

Consider a codeword of length n sent through the AWGN channel with noise level N . When received, the codeword vector variance is now N , and its mean is the codeword sent. The vector is very likely to be contained in a sphere of radius n ( N + ϵ ) around the codeword sent. If we decode by mapping every message received onto the codeword at the center of this sphere, then an error occurs only when the received vector is outside of this sphere, which is very unlikely.

Each codeword vector has an associated sphere of received codeword vectors which are decoded to it and each such sphere must map uniquely onto a codeword. Because these spheres therefore must not intersect, we are faced with the problem of sphere packing. How many distinct codewords can we pack into our n -bit codeword vector? The received vectors have a maximum energy of n ( P + N ) and therefore must occupy a sphere of radius n ( P + N ) . Each codeword sphere has radius n N . The volume of an n-dimensional sphere is directly proportional to r n , so the maximum number of uniquely decodeable spheres that can be packed into our sphere with transmission power P is:

( n ( P + N ) ) n 2 ( n N ) n 2 = 2 n 2 log ⁡ ( 1 + P / N )

By this argument, the rate R can be no more than 1 2 log ⁡ ( 1 + P / N ) .

Achievability

In this section, we show achievability of the upper bound on the rate from the last section.

A codebook, known to both encoder and decoder, is generated by selecting codewords of length n, i.i.d. Gaussian with variance P − ϵ and mean zero. For large n, the empirical variance of the codebook will be very close to the variance of its distribution, thereby avoiding violation of the power constraint probabilistically.

Received messages are decoded to a message in the codebook which is uniquely jointly typical. If there is no such message or if the power constraint is violated, a decoding error is declared.

Let X n ( i ) denote the codeword for message i , while Y n is, as before the received vector. Define the following three events:

Event U :the power of the received message is larger than P .
Event V : the transmitted and received codewords are not jointly typical.
Event E j : ( X n ( j ) , Y n ) is in A ϵ ( n ) , the typical set where i ≠ j , which is to say that the incorrect codeword is jointly typical with the received vector.

An error therefore occurs if U , V or any of the E i occur. By the law of large numbers, P ( U ) goes to zero as n approaches infinity, and by the joint Asymptotic Equipartition Property the same applies to P ( V ) . Therefore, for a sufficiently large n , both P ( U ) and P ( V ) are each less than ϵ . Since X n ( i ) and X n ( j ) are independent for i ≠ j , we have that X n ( i ) and Y n are also independent. Therefore, by the joint AEP, P ( E j ) = 2 − n ( I ( X ; Y ) − 3 ϵ ) . This allows us to calculate P e ( n ) , the probability of error as follows:

P e ( n ) ≤ P ( U ) + P ( V ) + ∑ j ≠ i P ( E j ) ≤ ϵ + ϵ + ∑ j ≠ i 2 − n ( I ( X ; Y ) − 3 ϵ ) ≤ 2 ϵ + ( 2 n R − 1 ) 2 − n ( I ( X ; Y ) − 3 ϵ ) ≤ 2 ϵ + ( 2 3 n ϵ ) 2 − n ( I ( X ; Y ) − R ) ≤ 3 ϵ

Therefore, as n approaches infinity, P e ( n ) goes to zero and R < I ( X ; Y ) − 3 ϵ . Therefore, there is a code of rate R arbitrarily close to the capacity derived earlier.

Coding theorem converse

Here we show that rates above the capacity C = 1 2 log ⁡ ( 1 + P N ) are not achievable.

Suppose that the power constraint is satisfied for a codebook, and further suppose that the messages follow a uniform distribution. Let W be the input messages and W ^ the output messages. Thus the information flows as:

W ⟶ X ( n ) ( W ) ⟶ Y ( n ) ⟶ W ^

Making use of Fano's inequality gives:

H ( W | W ^ ) ≤ 1 + n R P e ( n ) = n ϵ n where ϵ n → 0 as P e ( n ) → 0

Let X i be the encoded message of codeword index i. Then:

n R = H ( W ) = I ( W ; W ^ ) + H ( W | W ^ ) ≤ I ( W ; W ^ ) + n ϵ n ≤ I ( X ( n ) ; Y ( n ) ) + n ϵ n = h ( Y ( n ) ) − h ( Y ( n ) | X ( n ) ) + n ϵ n = h ( Y ( n ) ) − h ( Z ( n ) ) + n ϵ n ≤ ∑ i = 1 n h ( Y i ) − h ( Z ( n ) ) + n ϵ n ≤ ∑ i = 1 n I ( X i ; Y i ) + n ϵ n

Let P i be the average power of the codeword of index i:

P i = 1 2 n R ∑ w x i 2 ( w )

Where the sum is over all input messages w . X i and Z i are independent, thus the expectation of the power of Y i is, for noise level N :

E ( Y i 2 ) = P i + N

And, if Y i is normally distributed, we have that

h ( Y i ) ≤ 1 2 log ⁡ 2 π e ( P i + N )

Therefore,

n R ≤ ∑ ( h ( Y i ) − h ( Z i ) ) + n ϵ n ≤ ∑ ( 1 2 log ⁡ ( 2 π e ( P i + N ) ) − 1 2 log ⁡ ( 2 π e N ) ) + n ϵ n = ∑ 1 2 log ⁡ ( 1 + P i N ) + n ϵ n

We may apply Jensen's equality to log ⁡ ( 1 + x ) , a concave (downward) function of x, to get:

1 n ∑ i = 1 n 1 2 log ⁡ ( 1 + P i N ) ≤ 1 2 log ⁡ ( 1 + 1 n ∑ i = 1 n P i N )

Because each codeword individually satisfies the power constraint, the average also satisfies the power constraint. Therefore,

1 n ∑ i = 1 n P i N

Which we may apply to simplify the inequality above and get:

1 2 log ⁡ ( 1 + 1 n ∑ i = 1 n P i N ) ≤ 1 2 log ⁡ ( 1 + P N )

Therefore, it must be that R ≤ 1 2 log ⁡ ( 1 + P N ) + ϵ n . Therefore, R must be less than a value arbitrarily close to the capacity derived earlier, as ϵ n → 0 .

Effects in time domain

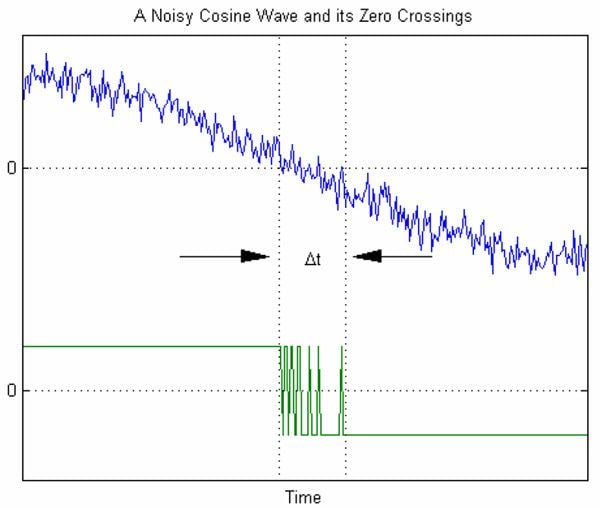
In serial data communications, the AWGN mathematical model is used to model the timing error caused by random jitter (RJ).

The graph to the right shows an example of timing errors associated with AWGN. The variable Δt represents the uncertainty in the zero crossing. As the amplitude of the AWGN is increased, the signal-to-noise ratio decreases. This results in increased uncertainty Δt.

When affected by AWGN, The average number of either positive going or negative going zero-crossings per second at the output of a narrow bandpass filter when the input is a sine wave is:

p o s i t i v e z e r o c r o s s i n g s s e c o n d = n e g a t i v e z e r o c r o s s i n g s s e c o n d = f 0 S N R + 1 + B 2 12 f 0 2 S N R + 1

Where

f₀ = the center frequency of the filter

B = the filter bandwidth

SNR = the signal-to-noise power ratio in linear terms

Effects in phasor domain

In modern communication systems, bandlimited AWGN cannot be ignored. When modeling bandlimited AWGN in the phasor domain, statistical analysis reveals that the amplitudes of the real and imaginary contributions are independent variables which follow the Gaussian distribution model. When combined, the resultant phasor's magnitude is a Rayleigh distributed random variable while the phase is uniformly distributed from 0 to 2π.

The graph to the right shows an example of how bandlimited AWGN can affect a coherent carrier signal. The instantaneous response of the Noise Vector cannot be precisely predicted, however its time-averaged response can be statistically predicted. As shown in the graph, we confidently predict that the noise phasor will reside inside the 1σ circle about 38% of the time; the noise phasor will reside inside the 2σ circle about 86% of the time; and the noise phasor will reside inside the 3σ circle about 98% of the time.

References

Additive white Gaussian noise Wikipedia

(Text) CC BY-SA

Contents