 | ||
In five-dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a 5-hypercube (penteract) with alternated vertices truncated.
Contents
It was discovered by Thorold Gosset. Since it was the only semiregular 5-polytope (made of more than one type of regular facets), he called it a 5-ic semi-regular. E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as HM5 for a 5-dimensional half measure polytope.
Coxeter named this polytope as 121 from its Coxeter diagram, which has branches of length 2, 1 and 1 with a ringed node on one of the short branches, and Schläfli symbol
It exists in the k21 polytope family as 121 with the Gosset polytopes: 221, 321, and 421.
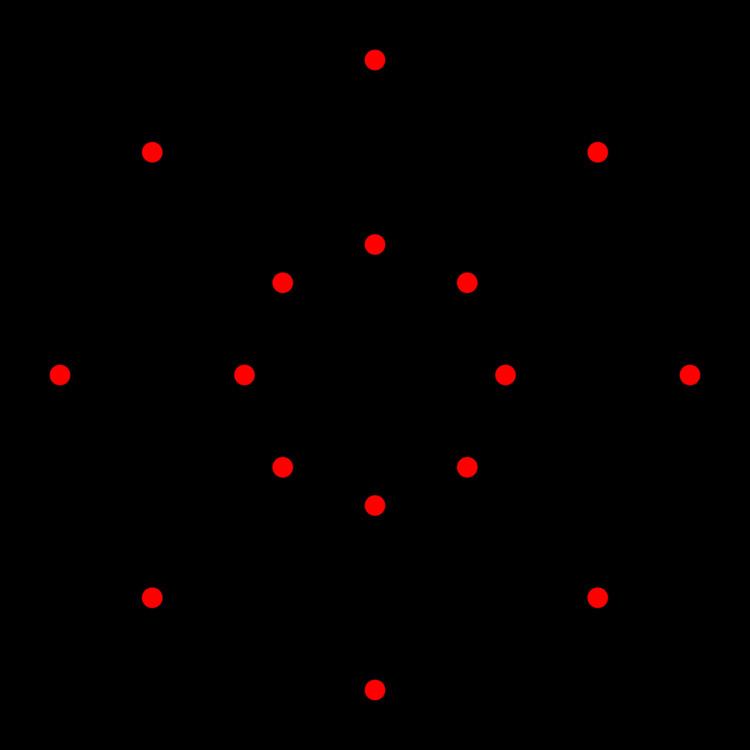
The graph formed by the vertices and edges of the demipenteract is sometimes called the Clebsch graph, though that name sometimes refers to the folded cube graph of order five instead.
Cartesian coordinates
Cartesian coordinates for the vertices of a demipenteract centered at the origin and edge length 2√2 are alternate halves of the penteract:
(±1,±1,±1,±1,±1)with an odd number of plus signs.
Related polytopes
It is a part of a dimensional family of uniform polytopes called demihypercubes for being alternation of the hypercube family.
There are 23 Uniform 5-polytopes (uniform 5-polytopes) that can be constructed from the D5 symmetry of the demipenteract, 8 of which are unique to this family, and 15 are shared within the penteractic family.
The 5-demicube is third in a dimensional series of semiregular polytopes. Each progressive uniform polytope is constructed vertex figure of the previous polytope. Thorold Gosset identified this series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes (5-cells and 16-cells in the case of the rectified 5-cell). In Coxeter's notation the 5-demicube is given the symbol 121.
