 | ||
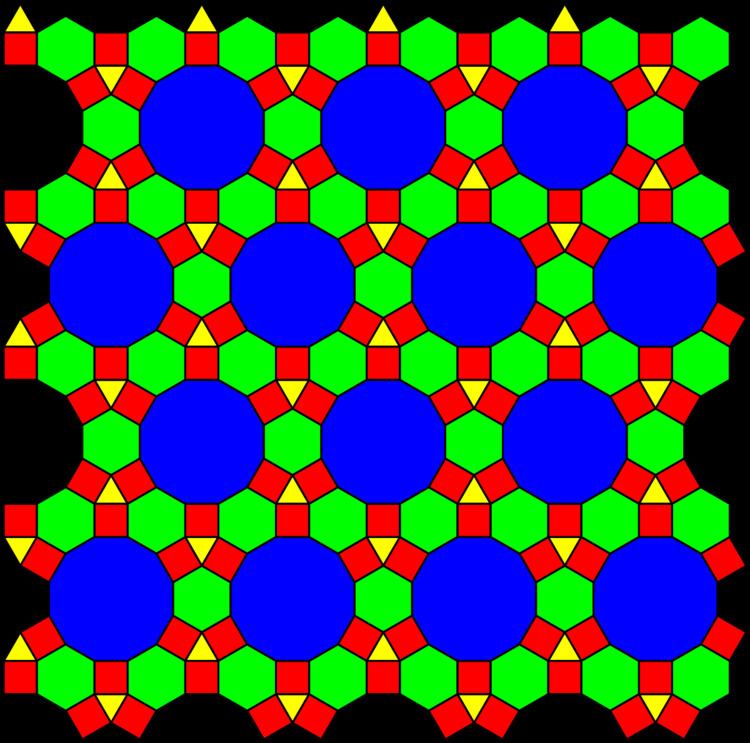
In geometry of the Euclidean plane, the 3-4-6-12 tiling is one of 20 2-uniform tilings of the Euclidean plane by regular polygons, containing regular triangles, squares, hexagons and dodecagons, arranged in two vertex configuration: 3.4.6.4 and 4.6.12.
Contents
It has hexagonal symmetry, p6m, [6,3], (*632). It is also called a demiregular tiling by some authors.
Geometry
Its two vertex configurations are shared with two 1-uniform tilings:
It can be seen as a type of diminished rhombitrihexagonal tiling, with dodecagons replacing periodic sets of hexagons and surrounding squares and triangles. This is similar to the Johnson solid, a diminished rhombicosidodecahedron, which is a rhombicosidodecahedron with faces removed, leading to new decagonal faces.
Related k-uniform tilings of regular polygons
The hexagons can be dissected into 6 triangles, and the dodecagaons can be dissected into triangles, hexagons and squares.
Dual tiling
The dual tiling has right triangle and kite faces, defined by face configurations: V3.4.6.4 and V4.6.12, and can be seen combining the deltoidal trihexagonal tiling and kisrhombille tilings.
