Zernike polynomials

Definitions

There are even and odd Zernike polynomials. The even ones are defined as

and the odd ones as

where m and n are nonnegative integers with n ≥ m, φ is the azimuthal angle, ρ is the radial distance 0 ≤ ρ ≤ 1 , and R^m_n are the radial polynomials defined below. Zernike polynomials have the property of being limited to a range of −1 to +1, i.e. | Z n m ( ρ , φ ) | ≤ 1 . The radial polynomials R^m_n are defined as

for n − m even, and are identically 0 for n − m odd.

Other representations

Rewriting the ratios of factorials in the radial part as products of binomials shows that the coefficients are integer numbers:

A notation as terminating Gaussian hypergeometric functions is useful to reveal recurrences, to demonstrate that they are special cases of Jacobi polynomials, to write down the differential equations, etc.:

for n − m even.

Noll's sequential indices

Applications often involve linear algebra, where integrals over products of Zernike polynomials and some other factor build the matrix elements. To enumerate the rows and columns of these matrices by a single index, a conventional mapping of the two indices n and m to a single index j has been introduced by Noll. The table of this association Z n m → Z j starts as follows (sequence A176988 in the OEIS)

The rule is that the even Z (with even azimuthal part m, cos ⁡ ( m φ ) ) obtain even indices j, the odd Z odd indices j. Within a given n, lower values of m obtain lower j.

Orthogonality

The orthogonality in the radial part reads

Orthogonality in the angular part is represented by

where ϵ m (sometimes called the Neumann factor because it frequently appears in conjunction with Bessel functions) is defined as 2 if m = 0 and 1 if m ≠ 0 . The product of the angular and radial parts establishes the orthogonality of the Zernike functions with respect to both indices if integrated over the unit disk,

where d 2 r = ρ d ρ d φ is the Jacobian of the circular coordinate system, and where n − m and n ′ − m ′ are both even.

A special value is

Zernike transform

Any sufficiently smooth real-valued phase field over the unit disk G ( ρ , φ ) can be represented in terms of its Zernike coefficients (odd and even), just as periodic functions find an orthogonal representation with the Fourier series. We have

where the coefficients can be calculated using inner products. On the space of L 2 functions on the unit disk, there is an inner product defined by

The Zernike coefficients can then be expressed as follows:

Alternatively, one can use the known values of phase function G on the circular grid to form a system of equations. The phase function is retrieved by the unknown-coefficient weighted product with (known values) of Zernike polynomial across the unit grid. Hence, coefficients can also be found by solving a linear system, for instance by matrix inversion. Fast algorithms to calculate the forward and inverse Zernike transform use symmetry properties of trigonometric functions, separability of radial and azimuthal parts of Zernike polynomials, and their rotational symmetries.

Symmetries

The parity with respect to reflection along the x axis is

The parity with respect to point reflection at the center of coordinates is

where ( − 1 ) m could as well be written ( − 1 ) n because n − m is even for the relevant, non-vanishing values. The radial polynomials are also either even or odd, depending on order n or m:

The periodicity of the trigonometric functions implies invariance if rotated by multiples of 2 π / m radian around the center:

Recurrence relations

The Zernike polynomials satisfy the following recurrence relation which depends neither on the degree nor on the azimuthal order of the radial polynomials:

From the definition of R n m it can be seen that R m m ( ρ ) = ρ m and R m + 2 m ( ρ ) = ( ( m + 2 ) ρ 2 − ( m + 1 ) ) ρ m . The following three-term recurrence relation then allows to calculate all other R n m ( ρ ) :

The above relation is especially useful since the derivative of R n m can be calculated from two radial Zernike polynomials of adjacent degree:

Radial polynomials

The first few radial polynomials are:

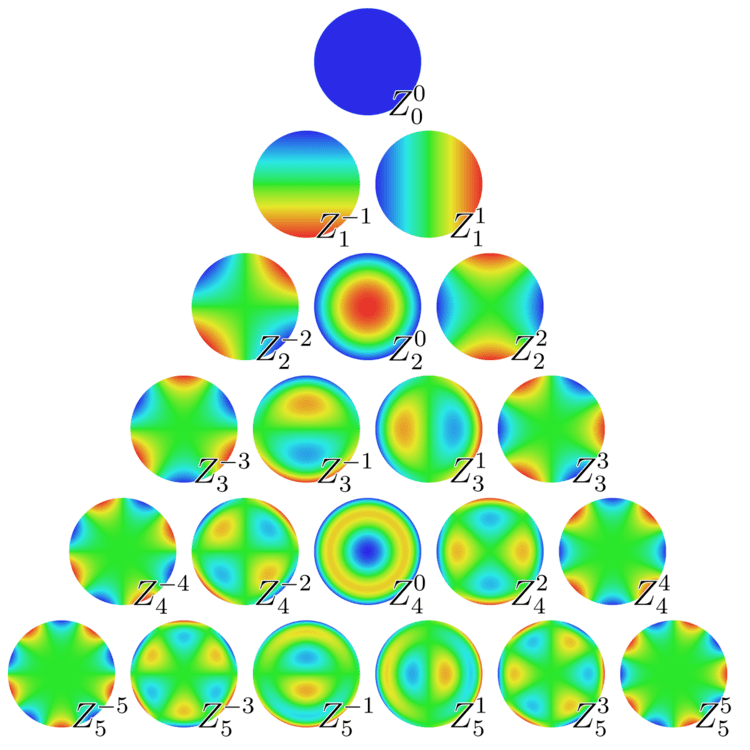
Zernike polynomials

The first few Zernike modes, ordered by Noll index j are shown below. They are normalized such that

Applications

The functions are a basis defined over the circular support area, typically the pupil planes in classical optical imaging at visible and infrared wavelengths through systems of lenses and mirrors of finite diameter. Their advantages are the simple analytical properties inherited from the simplicity of the radial functions and the factorization in radial and azimuthal functions; this leads, for example, to closed-form expressions of the two-dimensional Fourier transform in terms of Bessel functions. Their disadvantage, in particular if high n are involved, is the unequal distribution of nodal lines over the unit disk, which introduces ringing effects near the perimeter ρ ≈ 1 , which often leads attempts to define other orthogonal functions over the circular disk.

In precision optical manufacturing, Zernike polynomials are used to characterize higher-order errors observed in interferometric analyses, in order to achieve desired system performance.

In optometry and ophthalmology, Zernike polynomials are used to describe aberrations of the cornea or lens from an ideal spherical shape, which result in refraction errors.

They are commonly used in adaptive optics, where they can be used to effectively cancel out atmospheric distortion. Obvious applications for this are IR or visual astronomy and satellite imagery. For example, one of the Zernike terms (for m = 0, n = 2) is called "de-focus". By coupling the output from this term to a control system, an automatic focus can be implemented.

Another application of the Zernike polynomials is found in the Extended Nijboer–Zernike (ENZ) theory of diffraction and aberrations.

Zernike polynomials are widely used as basis functions of image moments. Since Zernike polynomials are orthogonal to each other, Zernike moments can represent properties of an image with no redundancy or overlap of information between the moments. Although Zernike moments are significantly dependent on the scaling and the translation of the object in a region of interest (ROI), their magnitudes are independent of the rotation angle of the object. Thus, they can be utilized to extract features from images that describe the shape characteristics of an object. For instance, Zernike moments are utilized as shape descriptors to classify benign and malignant breast masses. Zernike Moments also have been used to quantify shape of osteosarcoma cancer cell lines in single cell level. These quantifiers of cell shape have been used to distinguish between high invasive cancer cell lines from low invasive lines.

Higher dimensions

The concept translates to higher dimensions D if multinomials x 1 i x 2 j ⋯ x D k in Cartesian coordinates are converted to hyperspherical coordinates, ρ s , s ≤ D , multiplied by a product of Jacobi polynomials of the angular variables. In D = 3 dimensions, the angular variables are spherical harmonics, for example. Linear combinations of the powers ρ s define an orthogonal basis R n ( l ) ( ρ ) satisfying

(Note that a factor 2 n + D is absorbed in the definition of R here, whereas in D = 2 the normalization is chosen slightly differently. This is largely a matter of taste, depending on whether one wishes to maintain an integer set of coefficients or prefers tighter formulas if the orthogonalization is involved.) The explicit representation is

for even n − l ≥ 0 , else identical to zero.