Wrapped normal distribution - Alchetron, the free social encyclopedia



Parameters μ {\displaystyle \mu } real σ > 0 {\displaystyle \sigma >0} Support θ ∈ {\displaystyle \theta \in } any interval of length 2π PDF 1 2 π ϑ ( θ − μ 2 π , i σ 2 2 π ) {\displaystyle {\frac {1}{2\pi }}\vartheta \left({\frac {\theta -\mu }{2\pi }},{\frac {i\sigma ^{2}}{2\pi }}\right)} Mean μ {\displaystyle \mu } if support is on interval μ ± π {\displaystyle \mu \pm \pi } Median μ {\displaystyle \mu } if support is on interval μ ± π {\displaystyle \mu \pm \pi } Mode μ {\displaystyle \mu }

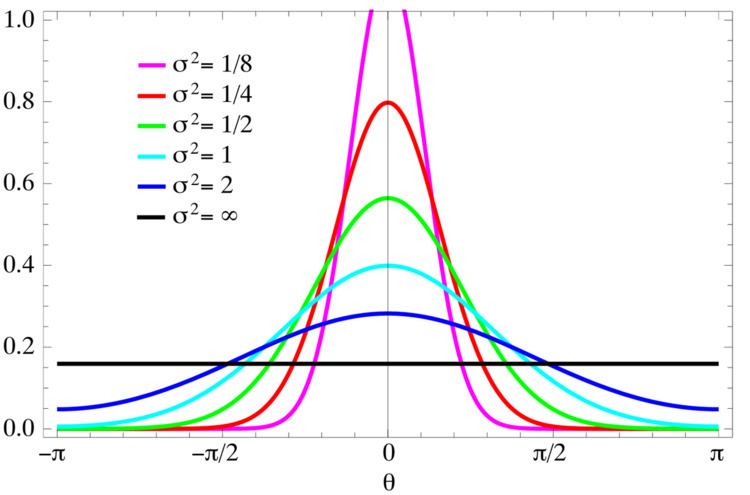
In probability theory and directional statistics, a wrapped normal distribution is a wrapped probability distribution that results from the "wrapping" of the normal distribution around the unit circle. It finds application in the theory of Brownian motion and is a solution to the heat equation for periodic boundary conditions. It is closely approximated by the von Mises distribution, which, due to its mathematical simplicity and tractability, is the most commonly used distribution in directional statistics.

Definition

The probability density function of the wrapped normal distribution is

f W N ( θ ; μ , σ ) = 1 σ 2 π ∑ k = − ∞ ∞ exp ⁡ [ − ( θ − μ + 2 π k ) 2 2 σ 2 ]

where μ and σ are the mean and standard deviation of the unwrapped distribution, respectively. Expressing the above density function in terms of the characteristic function of the normal distribution yields:

f W N ( θ ; μ , σ ) = 1 2 π ∑ n = − ∞ ∞ e − σ 2 n 2 / 2 + i n ( θ − μ ) = 1 2 π ϑ ( θ − μ 2 π , i σ 2 2 π ) ,

where ϑ ( θ , τ ) is the Jacobi theta function, given by

ϑ ( θ , τ ) = ∑ n = − ∞ ∞ ( w 2 ) n q n 2 where w ≡ e i π θ and q ≡ e i π τ .

The wrapped normal distribution may also be expressed in terms of the Jacobi triple product:

f W N ( θ ; μ , σ ) = 1 2 π ∏ n = 1 ∞ ( 1 − q n ) ( 1 + q n − 1 / 2 z ) ( 1 + q n − 1 / 2 / z ) .

where z = e i ( θ − μ ) and q = e − σ 2 .

Moments

In terms of the circular variable z = e i θ the circular moments of the wrapped Normal distribution are the characteristic function of the Normal distribution evaluated at integer arguments:

⟨ z n ⟩ = ∫ Γ e i n θ f W N ( θ ; μ , σ ) d θ = e i n μ − n 2 σ 2 / 2 .

where Γ is some interval of length 2 π . The first moment is then the average value of z, also known as the mean resultant, or mean resultant vector:

⟨ z ⟩ = e i μ − σ 2 / 2

The mean angle is

θ μ = A r g ⟨ z ⟩ = μ

and the length of the mean resultant is

R = | ⟨ z ⟩ | = e − σ 2 / 2

The circular standard deviation, which is a useful measure of dispersion for the wrapped Normal distribution and its close relative, the von Mises distribution is given by:

s = ln ⁡ ( 1 / R 2 ) = σ

Estimation of parameters

A series of N measurements z_n = e^iθ_n drawn from a wrapped normal distribution may be used to estimate certain parameters of the distribution. The average of the series z is defined as

z ¯ = 1 N ∑ n = 1 N z n

and its expectation value will be just the first moment:

⟨ z ¯ ⟩ = e i μ − σ 2 / 2 .

In other words, z is an unbiased estimator of the first moment. If we assume that the mean μ lies in the interval [−π, π), then Arg z will be a (biased) estimator of the mean μ.

Viewing the z_n as a set of vectors in the complex plane, the R² statistic is the square of the length of the averaged vector:

R ¯ 2 = z ¯ z ∗ ¯ = ( 1 N ∑ n = 1 N cos ⁡ θ n ) 2 + ( 1 N ∑ n = 1 N sin ⁡ θ n ) 2

and its expected value is:

⟨ R ¯ 2 ⟩ = 1 N + N − 1 N e − σ 2

In other words, the statistic

R e 2 = N N − 1 ( R ¯ 2 − 1 N )

will be an unbiased estimator of e^−σ², and ln(1/R_e²) will be a (biased) estimator of σ²

Entropy

The information entropy of the wrapped normal distribution is defined as:

H = − ∫ Γ f W N ( θ ; μ , σ ) ln ⁡ ( f W N ( θ ; μ , σ ) ) d θ

where Γ is any interval of length 2 π . Defining z = e i ( θ − μ ) and q = e − σ 2 , the Jacobi triple product representation for the wrapped normal is:

f W N ( θ ; μ , σ ) = ϕ ( q ) 2 π ∏ m = 1 ∞ ( 1 + q m − 1 / 2 z ) ( 1 + q m − 1 / 2 z − 1 )

where ϕ ( q ) is the Euler function. The logarithm of the density of the wrapped normal distribution may be written:

ln ⁡ ( f W N ( θ ; μ , σ ) ) = ln ⁡ ( ϕ ( q ) 2 π ) + ∑ m = 1 ∞ ln ⁡ ( 1 + q m − 1 / 2 z ) + ∑ m = 1 ∞ ln ⁡ ( 1 + q m − 1 / 2 z − 1 )

Using the series expansion for the logarithm:

ln ⁡ ( 1 + x ) = − ∑ k = 1 ∞ ( − 1 ) k k x k

the logarithmic sums may be written as:

∑ m = 1 ∞ ln ⁡ ( 1 + q m − 1 / 2 z ± 1 ) = − ∑ m = 1 ∞ ∑ k = 1 ∞ ( − 1 ) k k q m k − k / 2 z ± k = − ∑ k = 1 ∞ ( − 1 ) k k q k / 2 1 − q k z ± k

so that the logarithm of density of the wrapped normal distribution may be written as:

ln ⁡ ( f W N ( θ ; μ , σ ) ) = ln ⁡ ( ϕ ( q ) 2 π ) − ∑ k = 1 ∞ ( − 1 ) k k q k / 2 1 − q k ( z k + z − k )

which is essentially a Fourier series in θ . Using the characteristic function representation for the wrapped normal distribution in the left side of the integral:

f W N ( θ ; μ , σ ) = 1 2 π ∑ n = − ∞ ∞ q n 2 / 2 z n

the entropy may be written:

H = − ln ⁡ ( ϕ ( q ) 2 π ) + 1 2 π ∫ Γ ( ∑ n = − ∞ ∞ ∑ k = 1 ∞ ( − 1 ) k k q ( n 2 + k ) / 2 1 − q k ( z n + k + z n − k ) ) d θ

which may be integrated to yield:

H = − ln ⁡ ( ϕ ( q ) 2 π ) + 2 ∑ k = 1 ∞ ( − 1 ) k k q ( k 2 + k ) / 2 1 − q k

References

Wrapped normal distribution Wikipedia

(Text) CC BY-SA

Contents

Definition

Moments

Estimation of parameters

Entropy

References