 | ||
Version space learning is a logical approach to machine learning, specifically binary classification. Version space learning algorithms search a predefined space of hypotheses, viewed as a set of logical sentences. Formally, the hypothesis space is a disjunction
Contents
(i.e., either hypothesis 1 is true, or hypothesis 2, or any subset of the hypotheses 1 through n). A version space learning algorithm is presented with examples, which it will use to restrict its hypothesis space; for each example x, the hypotheses that are inconsistent with x are removed from the space. This iterative refining of the hypothesis space is called the candidate elimination algorithm, the hypothesis space maintained inside the algorithm its version space.
The version space algorithm
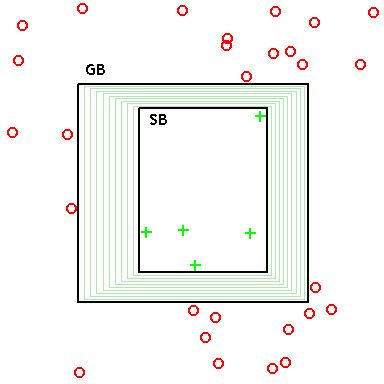
In settings where there is a generality-ordering on hypotheses, it is possible to represent the version space by two sets of hypotheses: (1) the most specific consistent hypotheses, and (2) the most general consistent hypotheses, where "consistent" indicates agreement with observed data.
The most specific hypotheses (i.e., the specific boundary SB) cover the observed positive training examples, and as little of the remaining feature space as possible. These hypotheses, if reduced any further, exclude a positive training example, and hence become inconsistent. These minimal hypotheses essentially constitute a (pessimistic) claim that the true concept is defined just by the positive data already observed: Thus, if a novel (never-before-seen) data point is observed, it should be assumed to be negative. (I.e., if data has not previously been ruled in, then it's ruled out.)
The most general hypotheses (i.e., the general boundary GB) cover the observed positive training examples, but also cover as much of the remaining feature space without including any negative training examples. These, if enlarged any further, include a negative training example, and hence become inconsistent. These maximal hypotheses essentially constitute a (optimistic) claim that the true concept is defined just by the negative data already observed: Thus, if a novel (never-before-seen) data point is observed, it should be assumed to be positive. (I.e., if data has not previously been ruled out, then it's ruled in.)
Thus, during learning, the version space (which itself is a set – possibly infinite – containing all consistent hypotheses) can be represented by just its lower and upper bounds (maximally general and maximally specific hypothesis sets), and learning operations can be performed just on these representative sets.
After learning, classification can be performed on unseen examples by testing the hypothesis learned by the algorithm. If the example is consistent with multiple hypotheses, a majority vote rule can be applied.
Historical background
The notion of version spaces was introduced by Mitchell in the early 1980s as a framework for understanding the basic problem of supervised learning within the context of solution search. Although the basic "candidate elimination" search method that accompanies the version space framework is not a popular learning algorithm, there are some practical implementations that have been developed (e.g., Sverdlik & Reynolds 1992, Hong & Tsang 1997, Dubois & Quafafou 2002).
A major drawback of version space learning is its inability to deal with noise: any pair of inconsistent examples can cause the version space to collapse, i.e., become empty, so that classification becomes impossible.
