 | ||
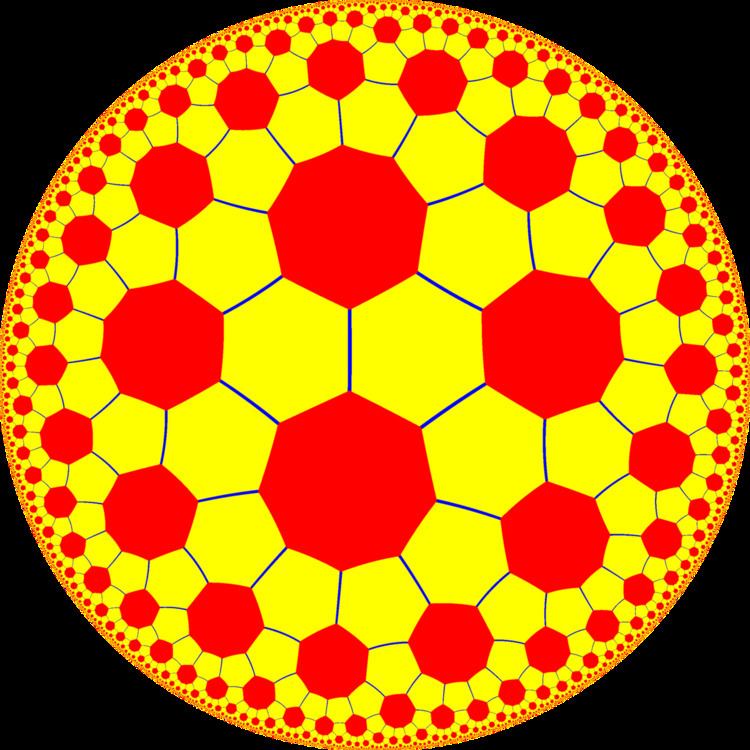
In geometry, the Truncated order-8 triangular tiling is a semiregular tiling of the hyperbolic plane. There are two hexagons and one octagon on each vertex. It has Schläfli symbol of t{3,8}.
Contents
Symmetry
The dual of this tiling represents the fundamental domains of *443 symmetry. It only has one subgroup 443, replacing mirrors with gyration points.
This symmetry can be doubled to 832 symmetry by adding a bisecting mirror to the fundamental domain.
Related tilings
From a Wythoff construction there are ten hyperbolic uniform tilings that can be based from the regular octagonal tiling.
It can also be generated from the (4 3 3) hyperbolic tilings:
This hyperbolic tiling is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (n.6.6), and [n,3] Coxeter group symmetry.
