 | ||
A transmission zero is a frequency at which the transfer function of a linear two-port network has zero transmission. Transmission zeroes at zero frequency and infinite frequency may be found in high-pass filters and low-pass filters respectively. Transmission zeroes at finite, non-zero frequency may be found in Band-stop filters, elliptic filters, and Type II Chebyshev filters. Transfer functions with both zero and infinite frequency can be found in band-pass filters. A transfer function may have multiple zeroes at the same frequency. A transfer function may have any number of transmission zeroes at zero frequency and infinite frequency, but transmission zeroes at finite non-zero frequency always come in conjugate pairs.
Contents
Generalized impedance converter
The circuit depicted to the left, based on a GIC (generalized impedance converter), has finite non-zero transmission zeroes.
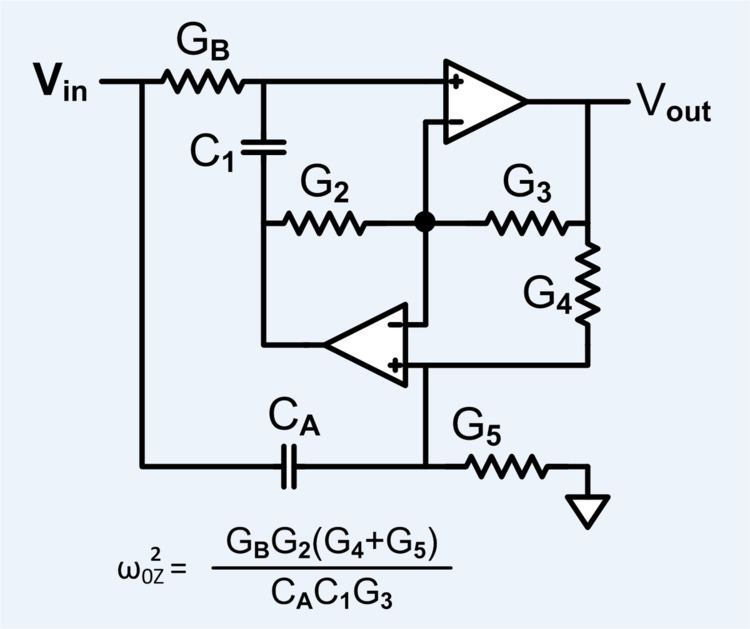
State variable derived
The filter circuit to the left has the following transfer function:
This circuit produces transmission zeroes at
