Taylor–Green vortex - Alchetron, The Free Social Encyclopedia

In fluid dynamics, the Taylor–Green vortex is an unsteady flow of a decaying vortex, which has an exact closed form solution of the incompressible Navier–Stokes equations in Cartesian coordinates. It is named after the British physicist and mathematician Geoffrey Ingram Taylor and his collaborator A. E. Green.

Original work

In the original work of Taylor and Green, a particular flow is analyzed in three spatial dimensions, with the three velocity components v = ( u , v , w ) at time t = 0 specified by

u = A cos ⁡ a x sin ⁡ b y sin ⁡ c z , v = B sin ⁡ a x cos ⁡ b y sin ⁡ c z , w = C sin ⁡ a x sin ⁡ b y cos ⁡ c z .

The continuity equation ∇ ⋅ v = 0 determines that A a + B b + C c = 0 . The small time behavior of the flow is then found through simplification of the incompressible Navier–Stokes equations using the initial flow to give a step-by-step solution as time progresses.

An exact solution in two spatial dimensions is known, and is presented below.

Incompressible Navier–Stokes equations

The incompressible Navier–Stokes equations in the absence of body force, and in two spatial dimensions, are given by

∂ u ∂ x + ∂ v ∂ y = 0 , ∂ u ∂ t + u ∂ u ∂ x + v ∂ u ∂ y = − 1 ρ ∂ p ∂ x + ν ( ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 ) , ∂ v ∂ t + u ∂ v ∂ x + v ∂ v ∂ y = − 1 ρ ∂ p ∂ y + ν ( ∂ 2 v ∂ x 2 + ∂ 2 v ∂ y 2 ) .

The first of the above equation represents the continuity equation and the other two represent the momentum equations.

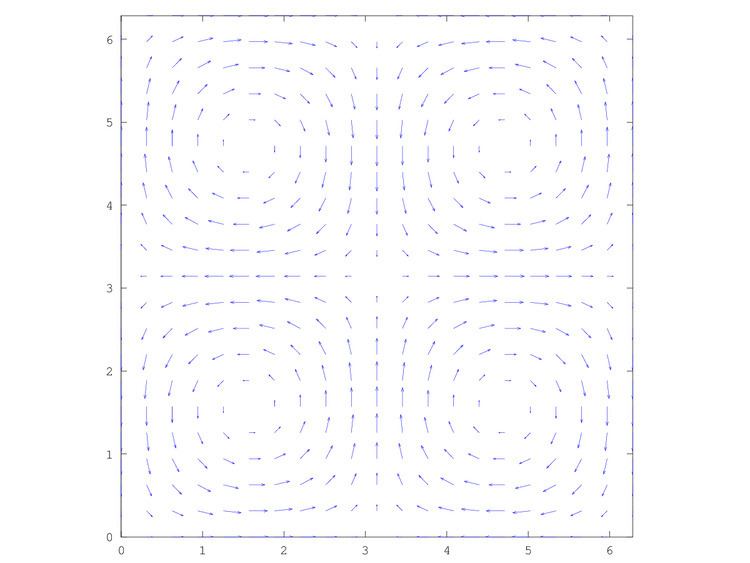
Taylor–Green vortex solution

In the domain 0 ≤ x , y ≤ 2 π , the solution is given by

u = cos ⁡ x sin ⁡ y F ( t ) , v = − sin ⁡ x cos ⁡ y F ( t ) ,

where F ( t ) = e − 2 ν t , ν being the kinematic viscosity of the fluid. Following the analysis of Taylor and Green for the two-dimensional situation, and for A = a = b = 1 , gives agreement with this exact solution, if the exponential is expanded as a Taylor series, i.e. F ( t ) = 1 − 2 ν t + O ( t 2 ) .

The pressure field p can be obtained by substituting the velocity solution in the momentum equations and is given by

p = − ρ 4 ( cos ⁡ 2 x + cos ⁡ 2 y ) F 2 ( t ) .

The stream function of the Taylor–Green vortex solution, i.e. which satisfies v = ∇ × ψ for flow velocity v , is

ψ = − cos ⁡ x cos ⁡ y F ( t ) z ^ .

Similarly, the vorticity, which satisfies ω = ∇ × v , is given by

ω = − 2 cos ⁡ x cos ⁡ y F ( t ) z ^ .

The Taylor–Green vortex solution may be used for testing and validation of temporal accuracy of Navier–Stokes algorithms.

References

Taylor–Green vortex Wikipedia

(Text) CC BY-SA

Contents

Original work

Incompressible Navier–Stokes equations

Taylor–Green vortex solution

References