 | ||
View the process involved with super resolution imaging
Super-resolution imaging (SR) is a class of techniques that enhance the resolution of an imaging system. In some SR techniques—termed optical SR—the diffraction limit of systems is transcended, while in others—geometrical SR—the resolution of digital imaging sensors is enhanced.
Contents
- View the process involved with super resolution imaging
- Basic concepts
- Optical or diffractive superresolution
- Geometrical or image processing superresolution
- Aliasing
- Technical implementations
- Research
- References
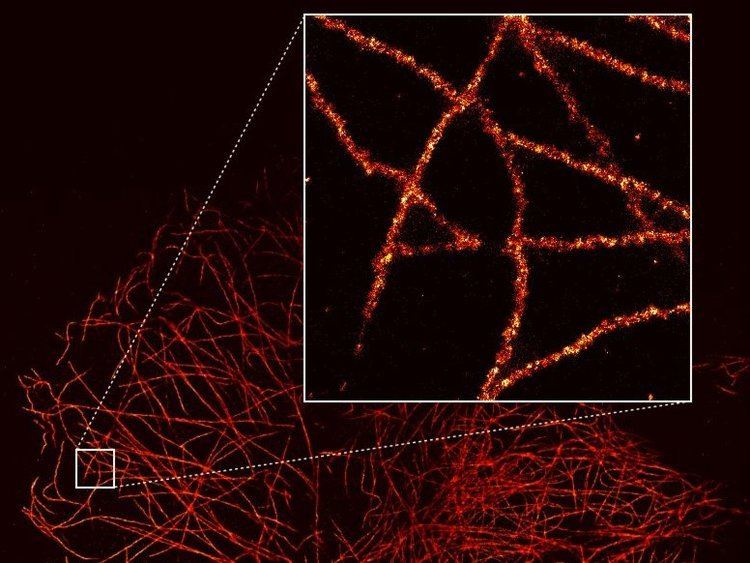
Super-resolution imaging techniques are used in general image processing and in super-resolution microscopy.
Basic concepts
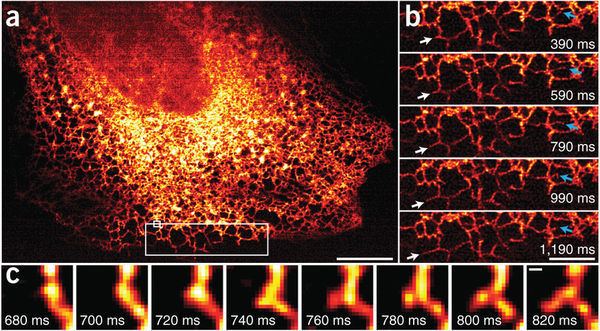
Because some of the ideas surrounding superresolution raise fundamental issues, there is need at the outset to examine the relevant physical and information-theoretical principles.
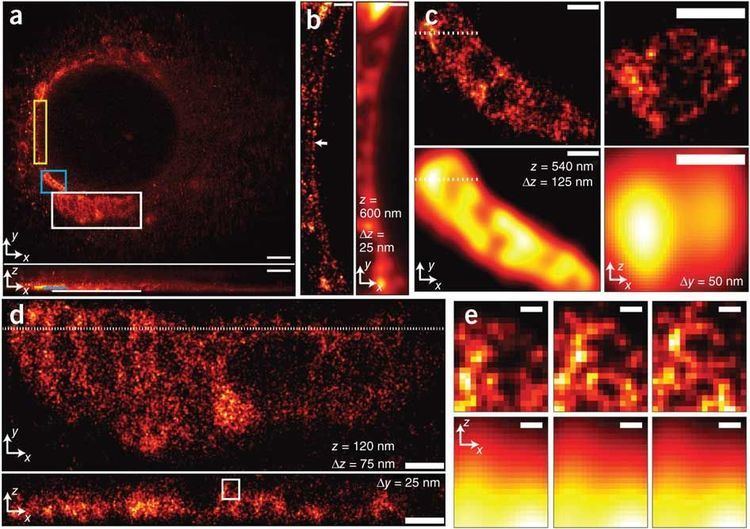
Diffraction Limit The detail of a physical object that an optical instrument can reproduce in an image has limits that are mandated by laws of physics, whether formulated by the diffraction equations in the wave theory of light or the Uncertainty Principle for photons in quantum mechanics. Information transfer can never be increased beyond this boundary, but packets outside the limits can be cleverly swapped for (or multiplexed with) some inside it. One does not so much “break” as “run around” the diffraction limit. New procedures probing electro-magnetic disturbances at the molecular level (in the so-called near field) remain fully consistent with Maxwell's equations.

A succinct expression of the diffraction limit is given in the spatial-frequency domain. In Fourier optics light distributions are expressed as superpositions of a series of grating light patterns in a range of fringe widths, technically spatial frequencies. It is generally taught that diffraction theory stipulates an upper limit, the cut-off spatial-frequency, beyond which pattern elements fail to be transferred into the optical image, i.e., are not resolved. But in fact what is set by diffraction theory is the width of the passband, not a fixed upper limit. No laws of physics are broken when a spatial frequency band beyond the cut-off spatial frequency is swapped for one inside it: this has long been implemented in dark-field microscopy. Nor are information-theoretical rules broken when superimposing several bands, disentangling them in the received image needs assumptions of object invariance during multiple exposures, i.e., the substitution of one kind of uncertainty for another.
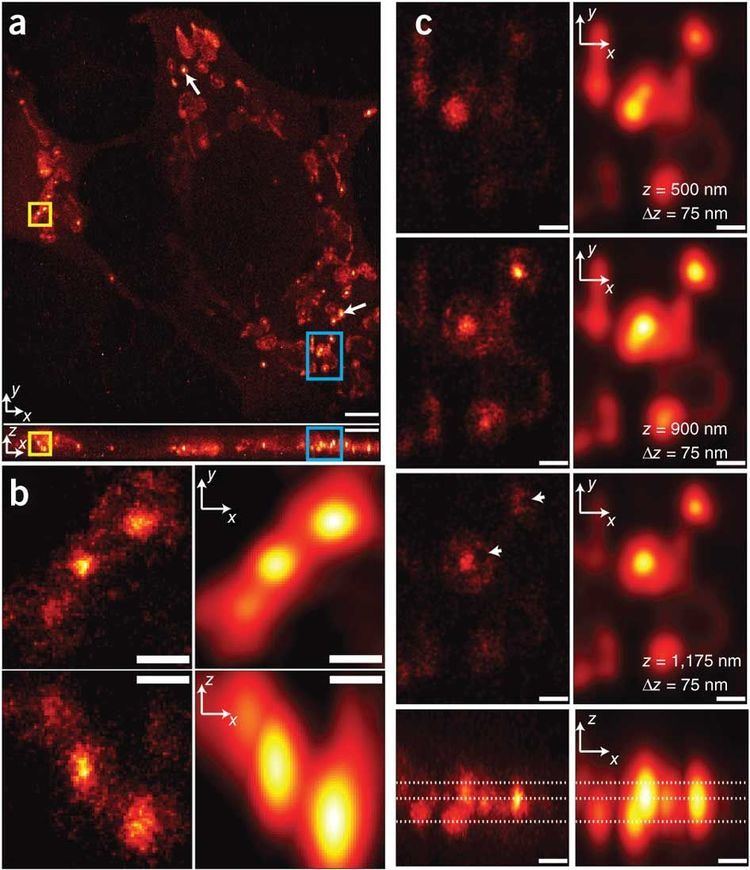
Information When the term superresolution is used in techniques of inferring object details from statistical treatment of the image within standard resolution limits, for example, averaging multiple exposures, it involves an exchange of one kind of information (extracting signal from noise) for another (the assumption that the target has remained invariant).

Resolution and localization True resolution involves the distinction of whether a target, e.g. a star or a spectral line, is single or double, ordinarily requiring separable peaks in the image. When a target is known to be single, its location can be determined with higher precision than the image width by finding the centroid (center of gravity) of its image light distribution. The word ultra-resolution had been proposed for this process but it did not catch on, and the high-precision localization procedure is typically referred to as superresolution.
In summary: The technical achievements of enhancing the performance of imaging-forming and –sensing devices now classified as superresolution utilize to the fullest but always stay within the bounds imposed by the laws of physics and information theory.
Optical or diffractive superresolution
Substituting spatial-frequency bands. Though the bandwidth allowable by diffraction is fixed, it can be positioned anywhere in the spatial-frequency spectrum. Dark-field illumination in microscopy is an example. See also aperture synthesis.
Geometrical or image-processing superresolution
Aliasing
Geometrical SR reconstruction algorithms are possible if and only if the input low resolution images have been under-sampled and therefore contain aliasing. Because of this aliasing, the high-frequency content of the desired reconstruction image is embedded in the low-frequency content of each of the observed images. Given a sufficient number of observation images, and if the set of observations vary in their phase (i.e. if the images of the scene are shifted by a sub-pixel amount), then the phase information can be used to separate the aliased high-frequency content from the true low-frequency content, and the full-resolution image can be accurately reconstructed.
In practice, this frequency-based approach is not used for reconstruction, but even in the case of spatial approaches (e.g. shift-add fusion), the presence of aliasing is still a necessary condition for SR reconstruction.
Technical implementations
There are both single-frame and multiple-frame variants of SR. Multiple-frame SR uses the sub-pixel shifts between multiple low resolution images of the same scene. It creates an improved resolution image fusing information from all low resolution images, and the created higher resolution images are better descriptions of the scene. Single-frame SR methods attempt to magnify the image without introducing blur. These methods use other parts of the low resolution images, or other unrelated images, to guess what the high-resolution image should look like. Algorithms can also be divided by their domain: frequency or space domain. Originally, super-resolution methods worked well only on grayscale images, but researchers have found methods to adapt them to color camera images. Recently, the use of super-resolution for 3D data has also been shown.
Research
There is promising research on using deep convolutional networks to perform super-resolution.
