 | ||
In geometry, a straight skeleton is a method of representing a polygon by a topological skeleton. It is similar in some ways to the medial axis but differs in that the skeleton is composed of straight line segments, while the medial axis of a polygon may involve parabolic curves.
Contents
Straight skeletons were first defined for simple polygons by Aichholzer et al. (1995), and generalized to planar straight-line graphs by Aichholzer & Aurenhammer (1996). In their interpretation as projection of roof surfaces, they are already extensively discussed by G. A. Peschka (1877).
Definition
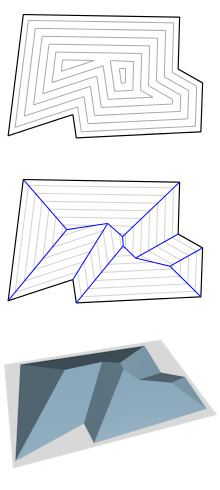
The straight skeleton of a polygon is defined by a continuous shrinking process in which the edges of the polygon are moved inwards parallel to themselves at a constant speed. As the edges move in this way, the vertices where pairs of edges meet also move, at speeds that depend on the angle of the vertex. If one of these moving vertices collides with a nonadjacent edge, the polygon is split in two by the collision, and the process continues in each part. The straight skeleton is the set of curves traced out by the moving vertices in this process. In the illustration the top figure shows the shrinking process and the middle figure depicts the straight skeleton in blue.
Algorithms
The straight skeleton may be computed by simulating the shrinking process by which it is defined; a number of variant algorithms for computing it have been proposed, differing in the assumptions they make on the input and in the data structures they use for detecting combinatorial changes in the input polygon as it shrinks.
Applications
Each point within the input polygon can be lifted into three-dimensional space by using the time at which the shrinking process reaches that point as the z-coordinate of the point. The resulting three-dimensional surface has constant height on the edges of the polygon, and rises at constant slope from them except for the points of the straight skeleton itself, where surface patches at different angles meet. In this way, the straight skeleton can be used as the set of ridge lines of a building roof, based on walls in the form of the initial polygon. The bottom figure in the illustration depicts a surface formed from the straight skeleton in this way.
Demaine, Demaine and Lubiw used the straight skeleton as part of a technique for folding a sheet of paper so that a given polygon can be cut from it with a single straight cut (the fold-and-cut theorem), and related origami design problems.
Barequet et al. use straight skeletons in an algorithm for finding a three-dimensional surface that interpolates between two given polygonal chains.
Tănase and Veltkamp propose to decompose concave polygons into unions of convex regions using straight skeletons, as a preprocessing step for shape matching in image processing.
Bagheri and Razzazi use straight skeletons to guide vertex placement in a graph drawing algorithm in which the graph drawing is constrained to lie inside a polygonal boundary.
The straight skeleton can also be used to construct an offset curve of a polygon, with mitered corners, analogously to the construction of an offset curve with rounded corners formed from the medial axis. Tomoeda and Sugihara apply this idea in the design of signage, visible from wide angles, with an illusory appearance of depth. Similarly, Asente and Carr use straight skeletons to design color gradients that match letter outlines or other shapes.
As with other types of skeleton such as the medial axis, the straight skeleton can be used to collapse a two-dimensional area to a simplified one-dimensional representation of the area. For instance, Haunert and Sester describe an application of this type for straight skeletons in geographic information systems, in finding the centerlines of roads.
Every tree with no degree-two vertices can be realized as the straight skeleton of a convex polygon. The convex hull of the roof shape corresponding to this straight skeleton forms a Steinitz realization of the Halin graph formed from the tree by connecting its leaves in a cycle.
Higher dimensions
Barequet et al. defined a version of straight skeletons for three-dimensional polyhedra, described algorithms for computing it, and analyzed its complexity on several different types of polyhedron.
Huber et al. investigated metric spaces under which the corresponding Voronoi diagrams and straight skeletons coincide. For two dimensions, the characterization of such metric spaces is complete. For higher dimensions, this method can be interpreted as a generalization of straight skeletons of certain input shapes to arbitrary dimensions by means of Voronoi diagrams.
