The Steiner conic or more precisely Steiner's generation of a conic, named after the Swiss mathematician Jakob Steiner, is an alternative method to define a non-degenerate projective conic section in a projective plane over a field.
The usual definition of a conic uses a quadratic form (see Quadric (projective geometry)). Another alternative definition of a conic uses a hyperbolic polarity. It is due to K. G. C. von Staudt and sometimes called a von Staudt conic. The disadvantage of von Staudt's definition is that it only works when the underlying field has odd characteristic (i.e., C h a r ≠ 2 ).
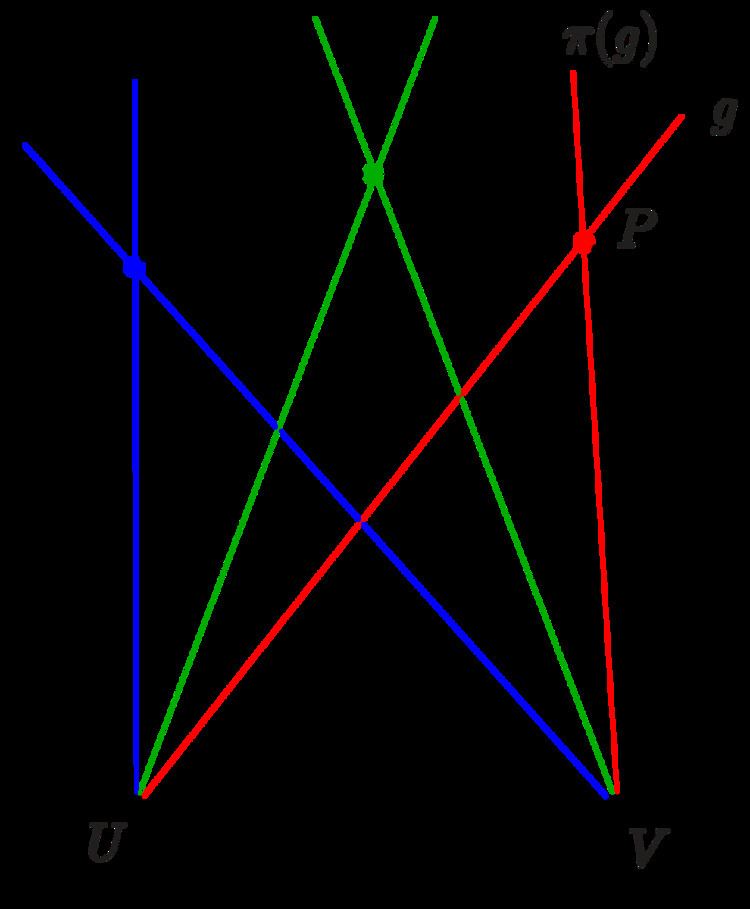
Given two pencils B ( U ) , B ( V ) of lines at two points U , V (all lines containing U and V resp.) and a projective but not perspective mapping π of B ( U ) onto B ( V ) . Then the intersection points of corresponding lines form a non-degenerate projective conic section (figure 1)A perspective mapping π of a pencil B ( U ) onto a pencil B ( V ) is a bijection (1-1 correspondence) such that corresponding lines intersect on a fixed line a , which is called the axis of the perspectivity π (figure 2).
A projective mapping is a finite sequence of perspective mappings.
Examples of commonly used fields are the real numbers R , the rational numbers Q or the complex numbers C . The construction also works over finite fields, providing examples in finite projective planes.
Remark: The fundamental theorem for projective planes states, that a projective mapping in a projective plane over a field (pappian plane) is uniquely determined by prescribing the images of three lines. That means that, for the Steiner generation of a conic section, besides two points U , V only the images of 3 lines have to be given. These 5 items (2 points, 3 lines) uniquely determine the conic section.
Remark: The notation "perspective" is due to the dual statement: The projection of the points on a line a from a center Z onto a line b is called a perspectivity (see below).
For the following example the images of the lines a , u , w (see picture) are given: π ( a ) = b , π ( u ) = w , π ( w ) = v . The projective mapping π is the product of the following perspective mappings π b , π a : 1) π b is the perspective mapping of the pencil at point U onto the pencil at point O with axis b . 2) π a is the perspective mapping of the pencil at point O onto the pencil at point V with axis a . First one should check that π = π a π b has the properties: π ( a ) = b , π ( u ) = w , π ( w ) = v . Hence for any line g the image π ( g ) = π a π b ( g ) can be constructed and therefore the images of an arbitrary set of points. The lines u and v contain only the conic points U and V resp.. Hence u and v are tangent lines of the generated conic section.
A proof that this method generates a conic section follows from switching to the affine restriction with line w as the line at infinity, point O as the origin of a coordinate system with points U , V as points at infinity of the x- and y-axis resp. and point E = ( 1 , 1 ) . The affine part of the generated curve appears to be the hyperbola y = 1 / x .
Remark:
- The Steiner generation of a conic section provides simple methods for the construction of ellipses, parabolas and hyperbolas which are commonly called the parallelogram methods.
- The figure that appears while constructing a point (figure 3) is the 4-point-degeneration of Pascal's theorem.
Definitions and the dual generation
Dualizing (see duality (projective geometry)) a projective plane means exchanging the points with the lines and the operations intersection and connecting. The dual structure of a projective plane is also a projective plane. The dual plane of a pappian plane is pappian and can also be coordinatized by homogenous coordinates. A nondegenerate dual conic section is analogously defined by a quadratic form.
A dual conic can be generated by Steiner's dual method:
Given the point sets of two lines u , v and a projective but not perspective mapping π of u onto v . Then the lines connecting corresponding points form a dual non-degenerate projective conic section.A perspective mapping π of the point set of a line u onto the point set of a line v is a bijection (1-1 correspondence) such that the connecting lines of corresponding points intersect at a fixed point Z , which is called the centre of the perspectivity π (see figure).
A projective mapping is a finite sequence of perspective mappings.
It is usual, when dealing with dual and common conic sections, to call the common conic section a point conic and the dual conic a line conic.
In the case that the underlying field has C h a r = 2 all the tangents of a point conic intersect in a point, called the knot (or nucleus) of the conic. Thus, the dual of a non-degenerate point conic is a subset of points of a dual line and not an oval curve (in the dual plane). So, only in the case that C h a r ≠ 2 is the dual of a non-degenerate point conic a non-degenerate line conic.
For the following example the images of the points A , U , W are given: π ( A ) = B , π ( U ) = W , π ( W ) = V . The projective mapping π can be represented by the product of the following perspectivities π B , π A :
1)
π B is the perspectivity of the point set of line
u onto the point set of line
o with centre
B .2)
π A is the perspectivity of the point set of line
o onto the point set of line
v with centre
A .
One easily checks that the projective mapping π = π A π B fulfills π ( A ) = B , π ( U ) = W , π ( W ) = V . Hence for any arbitrary point G the image π ( G ) = π A π B ( G ) can be constructed and line G π ( G ) ¯ is an element of a non degenerate dual conic section. Because the points U and V are contained in the lines u , v resp.,the points U and V are points of the conic and the lines u , v are tangents at U , V .