 | ||
Discretization of elliptic differential equations using sparse grids cristoph pflaum
Sparse grids are numerical techniques to represent, integrate or interpolate high dimensional functions. They were originally developed by the Russian mathematician Sergey A. Smolyak, a student of Lazar Lyusternik, and are based on a sparse tensor product construction. Computer algorithms for efficient implementations of such grids were later developed by Michael Griebel and Christoph Zenger.
Contents
- Discretization of elliptic differential equations using sparse grids cristoph pflaum
- Broke one sparse grids
- Curse of dimensionality
- Smolyaks quadrature rule
- References
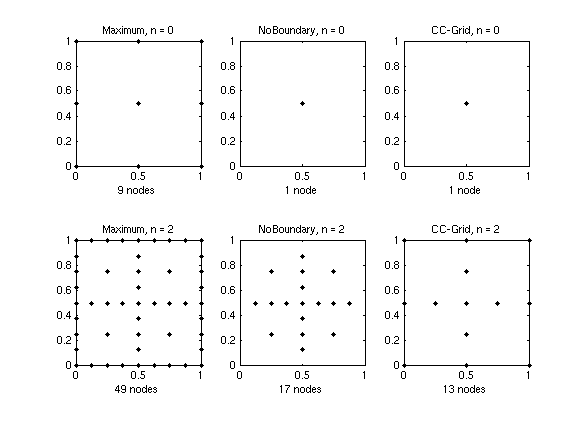
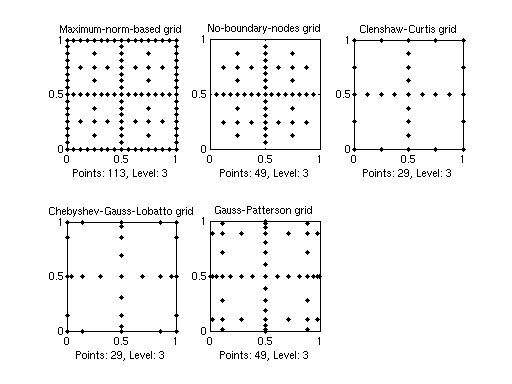
Broke one sparse grids
Curse of dimensionality
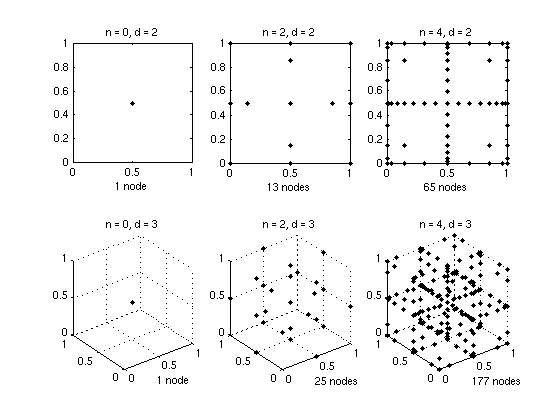
The standard way of representing multidimensional functions are tensor or full grids. The number of basis functions or nodes (grid points) that have to be stored and processed depend exponentially on the number of dimensions. Even with today's computational power it is not possible to process functions with more than 4 or 5 dimensions.

The curse of dimension is expressed in the order of the integration error that is made by a quadrature of level
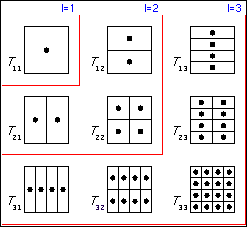
Smolyak's quadrature rule
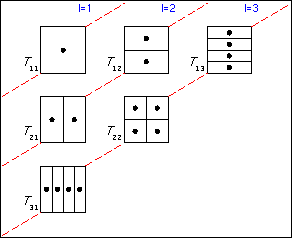
Smolyak found a computationally more efficient method of integrating multidimensional functions based on a univariate quadrature rule
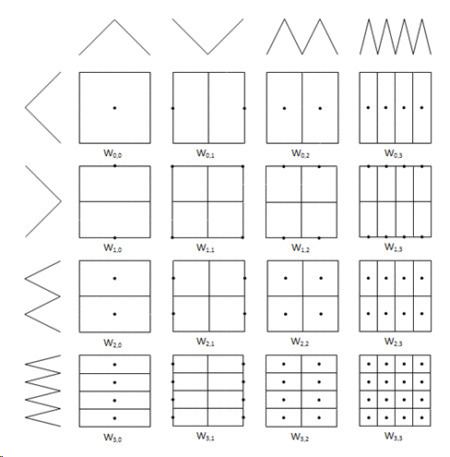
The index to
