Root test

Test

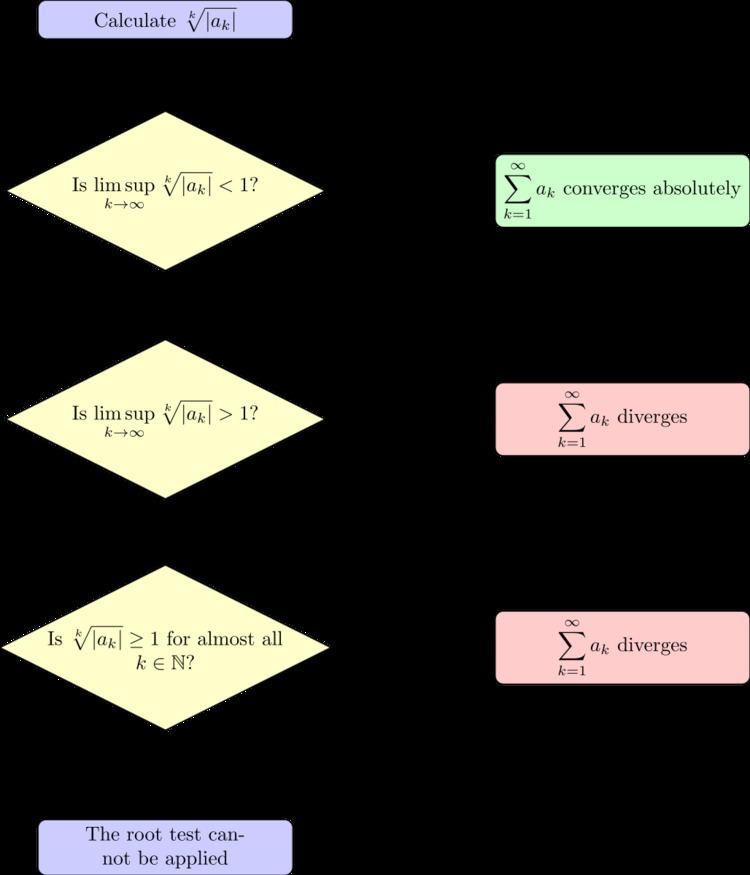
The root test was developed first by Augustin-Louis Cauchy who published it in his textbook Cours d'analyse (1821). Thus, it is sometimes known as the Cauchy root test or Cauchy's radical test. For a series

the root test uses the number

where "lim sup" denotes the limit superior, possibly ∞. Note that if

converges then it equals C and may be used in the root test instead.

The root test states that:

There are some series for which C = 1 and the series converges, e.g. ∑ 1 / n 2 , and there are others for which C = 1 and the series diverges, e.g. ∑ 1 / n .

Application to power series

This test can be used with a power series

where the coefficients c_n, and the center p are complex numbers and the argument z is a complex variable.

The terms of this series would then be given by a_n = c_n(z − p)ⁿ. One then applies the root test to the a_n as above. Note that sometimes a series like this is called a power series "around p", because the radius of convergence is the radius R of the largest interval or disc centred at p such that the series will converge for all points z strictly in the interior (convergence on the boundary of the interval or disc generally has to be checked separately). A corollary of the root test applied to such a power series is that the radius of convergence is exactly 1 / lim sup n → ∞ | c n | n , taking care that we really mean ∞ if the denominator is 0.

Proof

The proof of the convergence of a series Σa_n is an application of the comparison test. If for all n ≥ N (N some fixed natural number) we have | a n | n ≤ k < 1 , then | a n | ≤ k n < 1 . Since the geometric series ∑ n = N ∞ k n converges so does ∑ n = N ∞ | a n | by the comparison test. Hence Σa_n converges absolutely. Note that lim sup n → ∞ a n ≤ C < 1 implies that | a n | ≤ C + 1 2 < 1 for almost all n ∈ N .

If | a n | n > 1 for infinitely many n, then a_n fails to converge to 0, hence the series is divergent.

Proof of corollary: For a power series Σa_n = Σc_n(z − p)ⁿ, we see by the above that the series converges if there exists an N such that for all n ≥ N we have

equivalent to

for all n ≥ N, which implies that in order for the series to converge we must have | z − p | < 1 / | c n | n for all sufficiently large n. This is equivalent to saying

so R ≤ 1 / lim sup n → ∞ | c n | n . Now the only other place where convergence is possible is when

(since points > 1 will diverge) and this will not change the radius of convergence since these are just the points lying on the boundary of the interval or disc, so