 | ||
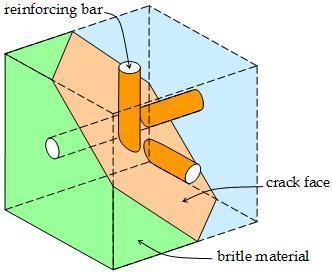
In solid mechanics, a reinforced solid is a brittle material that is reinforced by ductile bars or fibres. A common application is reinforced concrete. When the concrete cracks the tensile force in a crack is not carried any more by the concrete but by the steel reinforcing bars only. The reinforced concrete will continue to carry the load provided that sufficient reinforcement is present. A typical design problem is to find the smallest amount of reinforcement that can carry the stresses on a small cube (Fig. 1). This can be formulated as an optimization problem.
Contents
Optimization problem
The reinforcement is directed in the x, y and z direction. The reinforcement ratio is defined in a cross-section of a reinforcing bar as the reinforcement area
In case of reinforced concrete the reinforcement ratios are usually between 0.1% and 2%. The yield stress of the reinforcement is denoted by
This can be interpreted as the stress tensor of the composite material minus the stresses carried by the reinforcement at yielding. This formulation is accurate for reinforcement ratio's smaller than 5%. It is assumed that the brittle material has no tensile strength. (In case of reinforced concrete this assumption is necessary because the concrete has small shrinkage cracks.) Therefore, the principal stresses of the brittle material need to be compression. The principal stresses of a stress tensor are its eigenvalues.
The optimization problem is formulated as follows. Minimize
Solution
The solution to this problem can be presented in a form most suitable for hand calculations. It can be presented in graphical form. It can also be presented in a form most suitable for computer implementation. In this article the latter method is shown.
There are 12 possible reinforcement solutions to this problem, which are shown in the table below. Every row contains a possible solution. The first column contains the number of a solution. The second column gives conditions for which a solution is valid. Columns 3, 4 and 5 give the formulas for calculating the reinforcement ratios.
The algorithm for obtaining the right solution is simple. Compute the reinforcement ratios of each possible solution that fulfills the conditions. Further ignore solutions with a reinforcement ratio less than zero. Compute the values of
The formulas can be simply checked by substituting the reinforcement ratios in the brittle material stress tensor and calculating the invariants. The first invariant needs to be less than or equal to zero. The second invariant needs to be greater than or equal to zero. These provide the conditions in column 2. For solution 2 to 12, the third invariant needs to be zero.
Examples
The table below shows computed reinforcement ratios for 10 stress tensors. The applied reinforcement yield stress is
Extension
The above solution can be very useful to design reinforcement; however, it has some practical limitations. The following aspects can be included too if the problem is solved using convex optimization:
Degree of Utilization
Often, builders of reinforced concrete structures know, from experience, where to put reinforcing bars. Computer tools can support this by checking whether proposed reinforcement is sufficient. To this end the tension criterion,
The eigenvalues of
is rewritten into,
The eigenvalues of
The latter matrix is the utilization tensor. The largest eigenvalue of this tensor is the degree of utilization (unity check), which can be displayed in a contour plot of a structure for all load combinations related to the ultimate limit state.
For example, the stress at some location in a structure is
Combined compression and shear failure of the concrete can be checked with the Mohr-Coulomb criterion applied to the eigenvalues of the stress tensor of the brittle material.
where
Cracks in the concrete can be checked by replacing the yield stress
