 | ||
Regular semantics is a computing term which describes one type of guarantee provided by a data register shared by several processors in a parallel machine or in a network of computers working together. Regular semantics are defined for a variable with a single writer but multiple readers. These semantics are stronger than safe semantics but weaker than atomic semantics: they guarantee that there is a total order to the write operations which is consistent with real-time and that read operations return either the value of the last write completed before the read begins, or that of one of the writes which are concurrent with the read.
Contents
Example
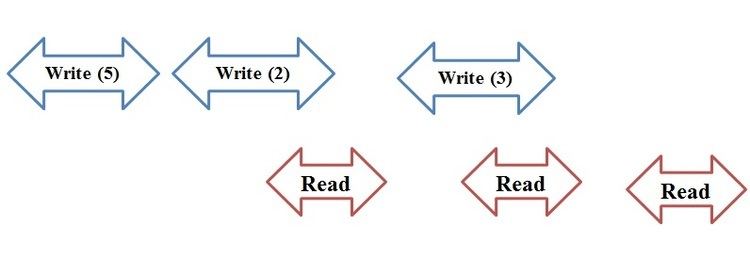
Regular semantics are weaker than linearizability. Consider the example shown below, where the horizontal axis represents time and the arrows represent the interval during which a read or write operation takes place. According to a regular register's definition, the third read should return 3 since the read operation is not concurrent with any write operation. On the other hand, the second read may return 2 or 3, and the first read may return either 5 or 2. The first read could return 3 and the second read could return 2. This behavior would not satisfy atomic semantics. Therefore, regular semantics is a weaker property than an atomic semantics. On the other hand, Lamport proved that a linearizable register may be implemented from registers with safe semantics, which are weaker than regular registers.
A Theorem from Regularity to Atomicity
A single-writer multi-reader (SWMR) atomic semantics is an SWMR regular register if any of its execution history H satisfies the following property: r1 and r2 are any two read invocations: (r1 →H r2) ⇒ ¬π(r2) →H π(r1)
Before we get into the proof,first we should know what does the new/old inversion mean.As it shown in the picture below,by looking at the execution we can see that the only difference between a regular execution and an atomic execution is when a = 0 and b = 1.In this execution,when we consider the two read invocations R.read() → a followed by R.read() → b, our first value(new value) is a = 0 while the second value(old value) is b=1.This is actually the main difference between atomacity and regularity.
The theorem above states that a Single writer multi-reader regular register without new or old inversion is an atomic register. By looking at the picture we can say that as R.read() → a →H R.read() → b and R.write(1) →H R.write(0), it is not possible to have π (R.read() → b) =R.write(1) and π (R.read() → a) = R.write(0) if the execution is atomic. For proving the theorem above,first we should prove that the register is safe,next we should show that the register is regular,and then at the end we should show that the register does not allow for new/old inversion which proves the atomicity. By the definition of the atomic register we know that a Single writer multiple reader atomic register is regular and satisfies the no new/old inversion property. So,we only need to show that a regular register with no new/old inversion is atomic.
We know that for any two read invocations (r1 and r2) when the register is regular and there is no new/old inversion (r1 →H r2) ⇒sn(π(r1)) ≤ sn(π(r2)). For any execution(M)there is a total order (S)which includes the same operation invocations.We can state that S is built as follow: we start from the total order on the write operations and we will insert the read operation as follow: first: Read operation(r) is inserted after the associated write operation(π(r)).Second: If two read operations (r1,r2) have the same (sn(r1)=sn(r2)) then first insert the operation which starts first in the execution. S includes all the operation invocation of M, from which it follows that S and M are equivalent. Since all the operations are ordered based on their sequence number,S is slightly a total order. Furthermore,this total order is an execution of M only adds an order on operations that are overlapping in M. If there is no overlapping between a read and write operations, there is no difference between the regularity and atomicity. Finally, we can state that S is legal since each read operation gets the last written value that comes before it in the total order. Therefore, the corresponding history is linearizable. Since this reasoning does not rely on a particular history H, it implies that the register is atomic. Since atomicity (linearizability) is a local property, we can state that a set of SWMR regular registers behave atomically as soon as each of them satisfies the no new/old inversion property.
