 | ||
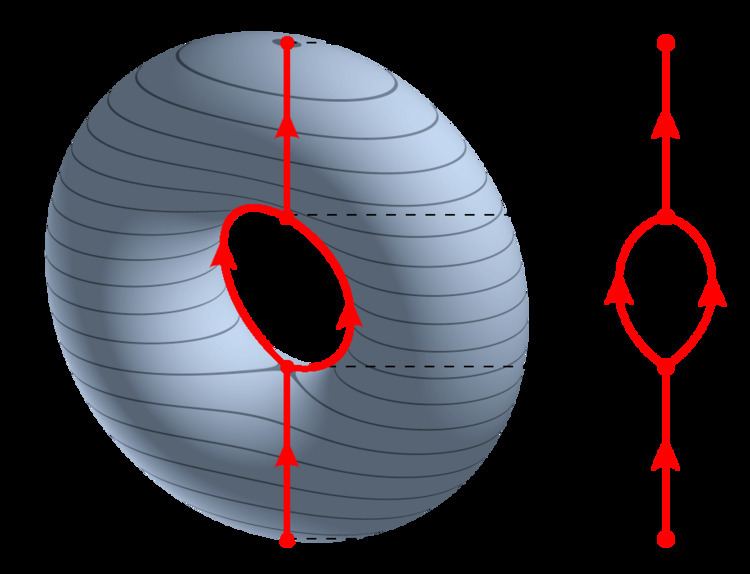
A Reeb graph (named after Georges Reeb) is a mathematical object reflecting the evolution of the level sets of a real-valued function on a manifold. Originally introduced by G.M. Adelson-Velskii and A.S. Kronrod and applied to analysis of Hilbert's thirteenth problem. Proposed by G. Reeb as a tool in Morse theory, Reeb graphs found a wide variety of applications in computational geometry and computer graphics, including computer aided geometric design, topology-based shape matching, topological simplification and cleaning, surface segmentation and parametrization, efficient computation of level sets, and geometrical thermodynamics. In a special case of a function on a flat space, the Reeb graph forms a polytree and is also called a contour tree.
Contents
Formal definition
Given a topological space X and a continuous function f: X → R, define an equivalence relation ∼ on X where p∼q whenever p and q belong to the same connected component of a single level set f−1(c) for some real c. The Reeb graph is the quotient space X /∼ endowed with the quotient topology.
Description for Morse functions
If f is a Morse function with distinct critical values, the Reeb graph can be described more explicitly. Its nodes, or vertices, correspond to the critical level sets f−1(c). The pattern in which the arcs, or edges, meet at the nodes/vertices reflects the change in topology of the level set f−1(t) as t passes through the critical value c. For example, if c is a minimum or a maximum of f, a component is created or destroyed; consequently, an arc originates or terminates at the corresponding node, which has degree 1. If c is a saddle point of index 1 and two components of f−1(t) merge at t = c as t increases, the corresponding vertex of the Reeb graph has degree 3 and looks like the letter "Y"; the same reasoning applies if the index of c is dim X−1 and a component of f−1(c) splits into two.
