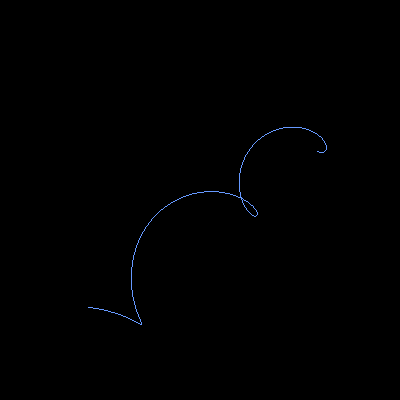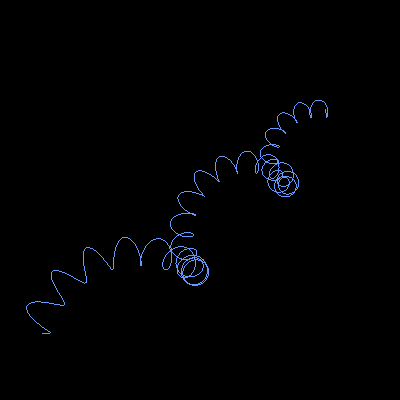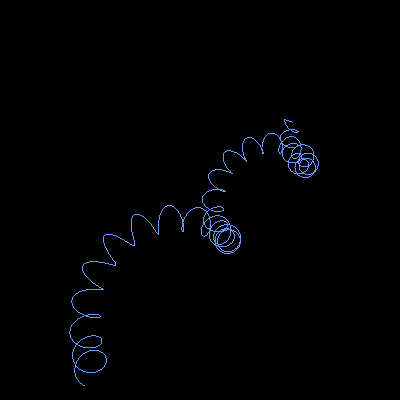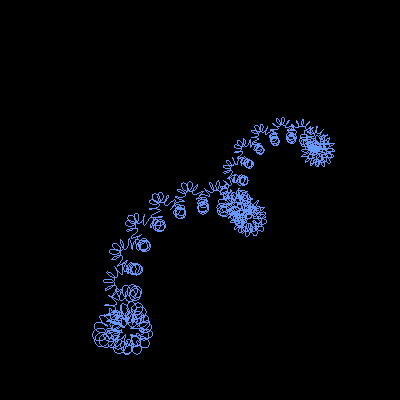A recursive wave is a self-similar curve in three-dimensional space that is constructed by iteratively adding a helix around the previous curve.
A recursive wave of depth n can be constructed as following:
where
and
Each wave at non-zero depth n is described by an amplitude A ( n ) , frequency f ( n ) and phase offset α ( n ) .
g n ( x ) represents a unit vector that is perpendicular to the previous curve at x . An arbitrary vector w → is chosen to be the fixed "rag" vector.
R is a function that rotates a vector A → around an axis defined by a vector B → by θ degrees. In this case it is expressed with quaternions.