 | ||
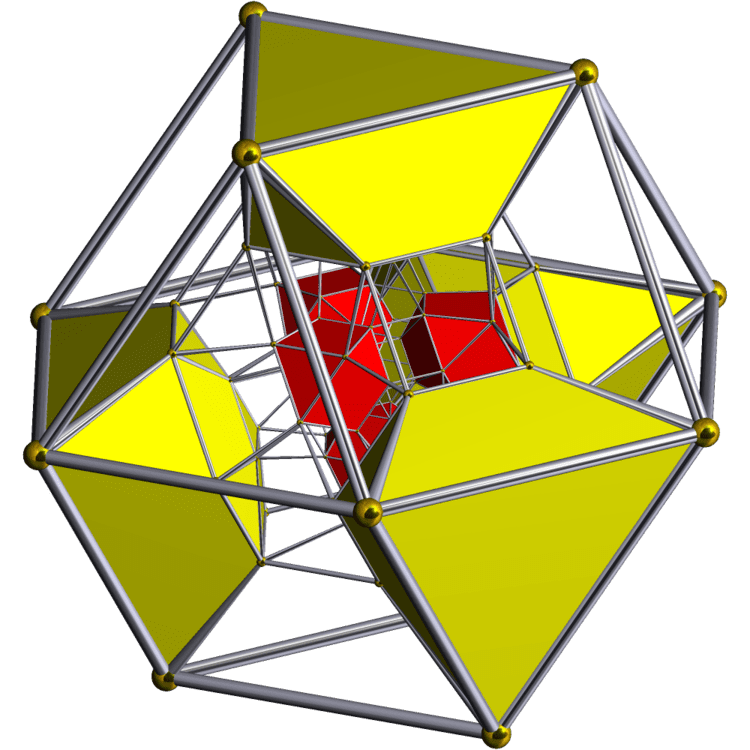
In geometry, the rectified 24-cell or rectified icositetrachoron is a uniform 4-dimensional polytope (or uniform 4-polytope), which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the 24-cell's cells to cubes or cuboctahedra.
Contents
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as tC24.
It can also be considered a cantellated 16-cell with the lower symmetries B4 = [3,3,4]. B4 would lead to a bicoloring of the cuboctahedral cells into 8 and 16 each. It is also called a runcicantellated demitesseract in a D4 symmetry, giving 3 colors of cells, 8 for each.
Cartesian coordinates
A rectified 24-cell having an edge length of √2 has vertices given by all permutations and sign permutations of the following Cartesian coordinates:
(0,1,1,2) [4!/2!×23 = 96 vertices]The dual configuration with edge length 2 has all coordinate and sign permutations of:
(0,2,2,2) [4×23 = 32 vertices](1,1,1,3) [4×24 = 64 vertices]Symmetry constructions
There are three different symmetry constructions of this polytope. The lowest
The vertex figure is a triangular prism, containing two cubes and three cuboctahedra. The three symmetries can be seen with 3 colored cuboctahedra in the lowest
Alternate names
Related uniform polytopes
The rectified 24-cell can also be derived as a cantellated 16-cell:
