Suvarna Garge (Editor)

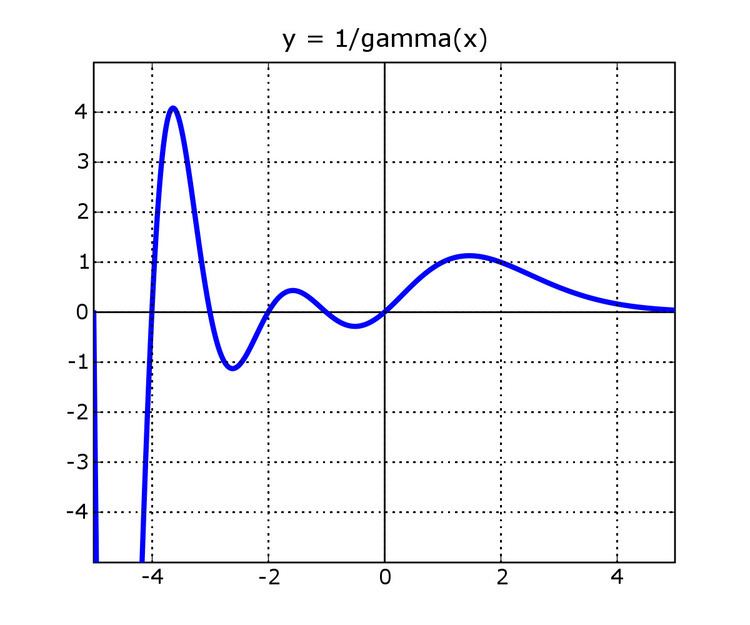
Reciprocal gamma function

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Reciprocal gamma function

In mathematics, the reciprocal gamma function is the function

Contents

f ( z ) = 1 Γ ( z ) ,

where Γ(z) denotes the gamma function. Since the gamma function is meromorphic and nonzero everywhere in the complex plane, its reciprocal is an entire function. As an entire function, it is of order 1 (meaning that log log | 1/Γ(z) | grows no faster than log | z |), but of infinite type (meaning that log | 1/Γ(z) | grows faster than any multiple of | z |, since its growth is approximately proportional to | z | log | z | in the left-hand plane).

The reciprocal is sometimes used as a starting point for numerical computation of the gamma function, and a few software libraries provide it separately from the regular gamma function.

Karl Weierstrass called the reciprocal gamma function the "factorielle" and used it in his development of the Weierstrass factorization theorem.

Infinite product expansion

Following from the infinite product definitions for the gamma function, due to Euler and Weierstrass respectively, we get the following infinite product expansion for the inverse gamma function:

1 Γ ( z ) = z ∏ n = 1 ∞ 1 + z n ( 1 + 1 n ) z 1 Γ ( z ) = z e γ z ∏ n = 1 ∞ ( 1 + z n ) e − z n

where γ ≈ 0.577216... is the Euler–Mascheroni constant. These expansions are valid for all complex numbers z.

Taylor series

Taylor series expansion around 0 gives

1 Γ ( z ) = z + γ z 2 + ( γ 2 2 − π 2 12 ) z 3 + ⋯

where γ is the Euler–Mascheroni constant. For k > 2, the coefficient ak for the zk term can be computed recursively as

a k = a 2 a k − 1 − ∑ j = 2 k − 1 ( − 1 ) j ζ ( j ) a k − j k − 1

where ζ(s) is the Riemann zeta function. For small values, this gives the following values:

Asymptotic expansion

As | z | goes to infinity at a constant arg(z) we have:

ln ⁡ ( 1 / Γ ( z ) ) ∼ − z ln ⁡ ( z ) + z + 1 2 ln ⁡ ( z 2 π ) − 1 12 z + 1 360 z 3 − 1 1260 z 5 for | arg ⁡ ( z ) | < π

Contour integral representation

An integral representation due to Hermann Hankel is

1 Γ ( z ) = i 2 π ∮ C ( − t ) − z e − t d t ,

where C is a path encircling 0 in the positive direction, beginning at and returning to positive infinity with respect for the branch cut along the positive real axis. According to Schmelzer & Trefethen, numerical evaluation of Hankel's integral is the basis of some of the best methods for computing the gamma function.

Integral along the real axis

Integration of the reciprocal gamma function along the positive real axis gives the value

∫ 0 ∞ 1 Γ ( x ) d x ≈ 2.80777024 ,

which is known as the Fransén–Robinson constant.

References

Reciprocal gamma function Wikipedia
(Text) CC BY-SA