Queueing theory

Spelling

The spelling "queueing" over "queuing" is typically encountered in the academic research field. In fact, one of the flagship journals of the profession is named Queueing Systems.

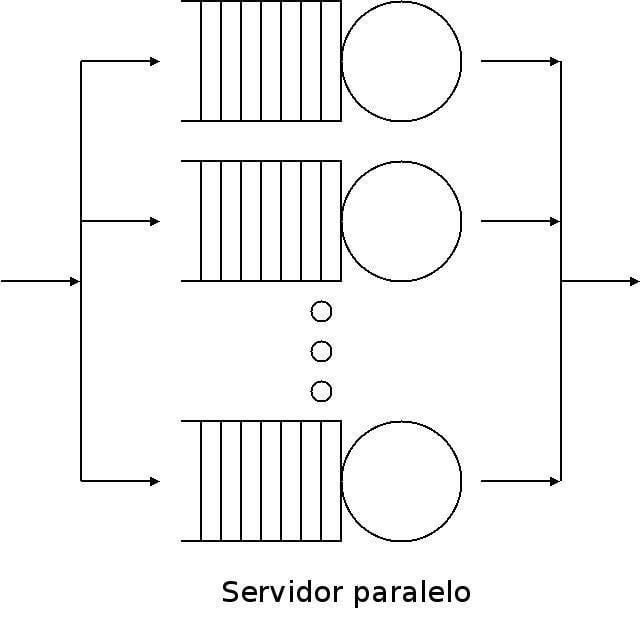
Single queueing nodes

Single queueing nodes are usually described using Kendall's notation in the form A/S/C where A describes the time between arrivals to the queue, S the size of jobs and C the number of servers at the node. Many theorems in queueing theory can be proved by reducing queues to mathematical systems known as Markov chains, first described by Andrey Markov in his 1906 paper.

Agner Krarup Erlang, a Danish engineer who worked for the Copenhagen Telephone Exchange, published the first paper on what would now be called queueing theory in 1909. He modeled the number of telephone calls arriving at an exchange by a Poisson process and solved the M/D/1 queue in 1917 and M/D/k queueing model in 1920. In Kendall's notation:

M stands for Markov or memoryless and means arrivals occur according to a Poisson process

D stands for deterministic and means jobs arriving at the queue require a fixed amount of service

k describes the number of servers at the queueing node (k = 1, 2,...). If there are more jobs at the node than there are servers then jobs will queue and wait for service

The M/M/1 queue is a simple model where a single server serves jobs that arrive according to a Poisson process and have exponentially distributed service requirements. In an M/G/1 queue the G stands for general and indicates an arbitrary probability distribution. The M/G/1 model was solved by Felix Pollaczek in 1930, a solution later recast in probabilistic terms by Aleksandr Khinchin and now known as the Pollaczek–Khinchine formula.

After the 1940s queueing theory became an area of research interest to mathematicians. In 1953 David George Kendall solved the GI/M/k queue and introduced the modern notation for queues, now known as Kendall's notation. In 1957 Pollaczek studied the GI/G/1 using an integral equation. John Kingman gave a formula for the mean waiting time in a G/G/1 queue: Kingman's formula.

The matrix geometric method and matrix analytic methods have allowed queues with phase-type distributed inter-arrival and service time distributions to be considered.

Problems such as performance metrics for the M/G/k queue remain an open problem.

Service disciplines

Various scheduling policies can be used at queuing nodes:

First in first out

This principle states that customers are served one at a time and that the customer that has been waiting the longest is served first.

Last in first out

This principle also serves customers one at a time, but the customer with the shortest waiting time will be served first. Also known as a stack.

Processor sharing

Service capacity is shared equally between customers.

Priority

Customers with high priority are served first. Priority queues can be of two types, non-preemptive (where a job in service cannot be interrupted) and preemptive (where a job in service can be interrupted by a higher-priority job). No work is lost in either model.

Shortest job first

The next job to be served is the one with the smallest size

Preemptive shortest job first

The next job to be served is the one with the original smallest size

Shortest remaining processing time

The next job to serve is the one with the smallest remaining processing requirement.

Service facility

Single server: customers line up and there is only one server

Parallel servers: customers line up and there are several servers

Tandem queue: there are many counters and customers can decide going where to queue

Customer’s behavior of waiting

Balking: customers deciding not to join the queue if it is too long

Jockeying: customers switch between queues if they think they will get served faster by doing so

Reneging: customers leave the queue if they have waited too long for service

Queueing networks

Networks of queues are systems in which a number of queues are connected by customer routing. When a customer is serviced at one node it can join another node and queue for service, or leave the network. For a network of m the state of the system can be described by an m–dimensional vector (x₁,x₂,...,x_m) where x_i represents the number of customers at each node.

The first significant results in this area were Jackson networks, for which an efficient product-form stationary distribution exists and the mean value analysis which allows average metrics such as throughput and sojourn times to be computed. If the total number of customers in the network remains constant the network is called a closed network and has also been shown to have a product–form stationary distribution in the Gordon–Newell theorem. This result was extended to the BCMP network where a network with very general service time, regimes and customer routing is shown to also exhibit a product-form stationary distribution. The normalizing constant can be calculated with the Buzen's algorithm, proposed in 1973.

Networks of customers have also been investigated, Kelly networks where customers of different classes experience different priority levels at different service nodes. Another type of network are G-networks first proposed by Erol Gelenbe in 1993: these networks do not assume exponential time distributions like the classic Jackson Network.

Example of M/M/1

Birth and Death process

A/B/C

A system of inter-arrival time and service time showed exponential distribution, we denoted M.

Let E represent the number of times of entering state n, and L represent the number of times of leaving state n. We have | E − L | ∈ { 0 , 1 } . When the system arrives at steady state, which means t, we have, therefore arrival rate=removed rate.

Balance equation

Routing algorithms

In discrete time networks where there is a constraint on which service nodes can be active at any time, the max-weight scheduling algorithm chooses a service policy to give optimal throughput in the case that each job visits only a single service node. In the more general case where jobs can visit more than one node, backpressure routing gives optimal throughput.

A network scheduler must choose a queuing algorithm, which affects the characteristics of the larger network.

Mean field limits

Mean field models consider the limiting behaviour of the empirical measure (proportion of queues in different states) as the number of queues (m above) goes to infinity. The impact of other queues on any given queue in the network is approximated by a differential equation. The deterministic model converges to the same stationary distribution as the original model.

Fluid limits

Fluid models are continuous deterministic analogs of queueing networks obtained by taking the limit when the process is scaled in time and space, allowing heterogeneous objects. This scaled trajectory converges to a deterministic equation which allows the stability of the system to be proven. It is known that a queueing network can be stable, but have an unstable fluid limit.

Heavy traffic/diffusion approximations

In a system with high occupancy rates (utilisation near 1) a heavy traffic approximation can be used to approximate the queueing length process by a reflected Brownian motion, Ornstein–Uhlenbeck process or more general diffusion process. The number of dimensions of the RBM is equal to the number of queueing nodes and the diffusion is restricted to the non-negative orthant.