 | ||
In computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack.
Contents
- Informal description
- Formal definition
- Example
- Understanding the computation process
- PDA and context free languages
- Generalized pushdown automaton GPDA
- Stack automaton
- Alternating pushdown automata
- References
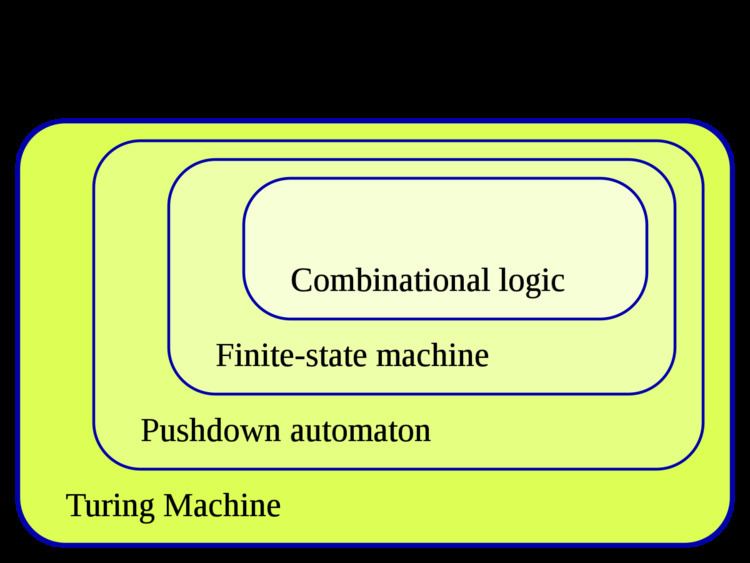
Pushdown automata are used in theories about what can be computed by machines. They are more capable than finite-state machines but less capable than Turing machines. Deterministic pushdown automata can recognize all deterministic context-free languages while nondeterministic ones can recognize all context-free languages, with the former often used in parser design.
The term "pushdown" refers to the fact that the stack can be regarded as being "pushed down" like a tray dispenser at a cafeteria, since the operations never work on elements other than the top element. A stack automaton, by contrast, does allow access to and operations on deeper elements. Stack automata can recognize a strictly larger set of languages than pushdown automata. A nested stack automaton allows full access, and also allows stacked values to be entire sub-stacks rather than just single finite symbols.
Informal description
A finite state machine just looks at the input signal and the current state: it has no stack to work with. It chooses a new state, the result of following the transition. A pushdown automaton (PDA) differs from a finite state machine in two ways:
- It can use the top of the stack to decide which transition to take.
- It can manipulate the stack as part of performing a transition.
A pushdown automaton reads a given input string from left to right. In each step, it chooses a transition by indexing a table by input symbol, current state, and the symbol at the top of the stack. A pushdown automaton can also manipulate the stack, as part of performing a transition. The manipulation can be to push a particular symbol to the top of the stack, or to pop off the top of the stack. The automaton can alternatively ignore the stack, and leave it as it is.
Put together: Given an input symbol, current state, and stack symbol, the automaton can follow a transition to another state, and optionally manipulate (push or pop) the stack.
If, in every situation, at most one such transition action is possible, then the automaton is called a deterministic pushdown automaton (DPDA). In general, several actions are possible, and the automaton is called a general, or nondeterministic, PDA. A given input string may drive a nondeterministic pushdown automaton to one of several configuration sequences; if one of them leads to an accepting configuration after reading the complete input string, the latter is said to belong to the language accepted by the automaton.
Formal definition
We use standard formal language notation:
A PDA is formally defined as a 7-tuple:
An element
In many texts the transition relation is replaced by an (equivalent) formalization, where
Here
Computations
In order to formalize the semantics of the pushdown automaton a description of the current situation is introduced. Any 3-tuple
In general pushdown automata are nondeterministic meaning that in a given instantaneous description
Computations of the pushdown automaton are sequences of steps. The computation starts in the initial state
Formally one defines
-
L ( M ) = { w ∈ Σ ∗ | ( q 0 , w , Z ) ⊢ M ∗ ( f , ε , γ ) withf ∈ F andγ ∈ Γ ∗ } (final state) -
N ( M ) = { w ∈ Σ ∗ | ( q 0 , w , Z ) ⊢ M ∗ ( q , ε , ε ) withq ∈ Q } (empty stack)
Here
For each single pushdown automaton these two languages need to have no relation: they may be equal but usually this is not the case. A specification of the automaton should also include the intended mode of acceptance. Taken over all pushdown automata both acceptance conditions define the same family of languages.
Theorem. For each pushdown automaton
Example
The following is the formal description of the PDA which recognizes the language
The transition relation
In words, the first two instructions say that in state p any time the symbol 5000000000000000000♠0 is read, one A is pushed onto the stack. Pushing symbol A on top of another A is formalized as replacing top A by AA (and similarly for pushing symbol A on top of a Z).
The third and fourth instructions say that, at any moment the automaton may move from state p to state q.
The fifth instruction says that in state q, for each symbol 7000100000000000000♠1 read, one A is popped.
Finally, the sixth instruction says that the machine may move from state q to accepting state r only when the stack consists of a single Z.
There seems to be no generally used representation for PDA. Here we have depicted the instruction
Understanding the computation process
The following illustrates how the above PDA computes on different input strings. The subscript M from the step symbol
PDA and context-free languages
Every context-free grammar can be transformed into an equivalent nondeterministic pushdown automaton. The derivation process of the grammar is simulated in a leftmost way. Where the grammar rewrites a nonterminal, the PDA takes the topmost nonterminal from its stack and replaces it by the right-hand part of a grammatical rule (expand). Where the grammar generates a terminal symbol, the PDA reads a symbol from input when it is the topmost symbol on the stack (match). In a sense the stack of the PDA contains the unprocessed data of the grammar, corresponding to a pre-order traversal of a derivation tree.
Technically, given a context-free grammar, the PDA has a single state, 1, and its transition relation is constructed as follows.
-
( 1 , ε , A , 1 , α ) for each ruleA → α (expand) -
( 1 , a , a , 1 , ε ) for each terminal symbola (match)
The PDA accepts by empty stack. Its initial stack symbol is the grammar's start symbol.
For a context-free grammar in Greibach normal form, defining (1,γ) ∈ δ(1,a,A) for each grammar rule A → aγ also yields an equivalent nondeterministic pushdown automaton.
The converse, finding a grammar for a given PDA, is not that easy. The trick is to code two states of the PDA into the nonterminals of the grammar.
Theorem. For each pushdown automaton
The language of strings accepted by a deterministic pushdown automaton is called a deterministic context-free language. Not all context-free languages are deterministic. As a consequence, the DPDA is a strictly weaker variant of the PDA and there exists no algorithm for converting a PDA to an equivalent DPDA, if such a DPDA exists.
A finite automaton with access to two stacks is a more powerful device, equivalent in power to a Turing machine. A linear bounded automaton is a device which is more powerful than a pushdown automaton but less so than a Turing machine.
Generalized pushdown automaton (GPDA)
A GPDA is a PDA which writes an entire string of some known length to the stack or removes an entire string from the stack in one step.
A GPDA is formally defined as a 6-tuple:
where
is the transition function.
Computation rules for a GPDA are the same as a PDA except that the
GPDA's and PDA's are equivalent in that if a language is recognized by a PDA, it is also recognized by a GPDA and vice versa.
One can formulate an analytic proof for the equivalence of GPDA's and PDA's using the following simulation:
Let
where
Construct the following transitions for the PDA:
Stack automaton
As a generalization of pushdown automata, Ginsburg, Greibach, and Harrison (1967) investigated stack automata, which may additionally step left or right in the input string (surrounded by special endmarker symbols to prevent slipping out), and step up or down in the stack in read-only mode. A stack automaton is called nonerasing if it never pops from the stack. The class of languages accepted by nondeterministic, nonerasing stack automata is NSPACE(n2), which is a superset of the context-sensitive languages. The class of languages accepted by deterministic, nonerasing stack automata is DSPACE(n⋅log(n)).
Alternating pushdown automata
An alternating pushdown automaton (APDA) is a pushdown automaton with a state set
States in
The model was introduced by Chandra, Kozen and Stockmeyer. Ladner, Lipton and Stockmeyer proved that this model is equivalent to EXPTIME i.e. a language is accepted by some APDA iff it can be decided by an exponential-time algorithm.
Aizikowitz and Kaminski introduced synchronized alternating pushdown automata (SAPDA) that are equivalent to conjunctive grammars in the same way as nondeterministic PDA are equivalent to context-free grammars.
