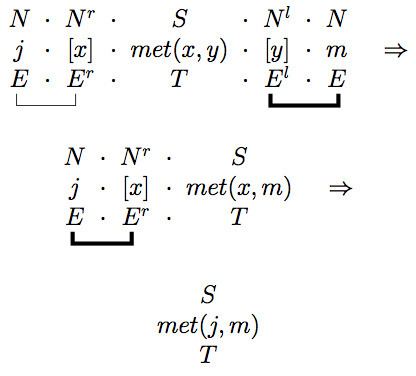Pregroup grammar - Alchetron, The Free Social Encyclopedia

Pregroup grammar (PG) is a grammar formalism intimately related to categorial grammars. Much like categorial grammar (CG), PG is a kind of type logical grammar. Unlike CG, however, PG does not have a distinguished function type. Rather, PG uses inverse types combined with its monoidal operation.

Definition of a pregroup

A pregroup is a partially ordered algebra ( A , 1 , ⋅ , − l , − r , ≤ ) such that ( A , 1 , ⋅ ) is a monoid, satisfying the following relations:

x l ⋅ x ≤ 1 x ⋅ x r ≤ 1 (contraction)

1 ≤ x ⋅ x l 1 ≤ x r ⋅ x (expansion)

The contraction and expansion relations are sometimes called Ajdukiewicz laws.

From this, it can be proven that the following equations hold:

1 l = 1 = 1 r

x l r = x = x r l

( x ⋅ y ) l = y l ⋅ x l ( x ⋅ y ) r = y r ⋅ x r

x l and x r are called the left and right adjoints of x, respectively.

The symbol ⋅ and ≤ are also written ⊗ and → respectively. In category theory, pregroups are also known as autonomous categories or (non-symmetric) compact closed categories. More typically, x ⋅ y will just be represented by adjacency, i.e. as x y .

Definition of a pregroup grammar

A pregroup grammar consists of a lexicon of words (and possibly morphemes) L, a set of atomic types T which freely generates a pregroup, and an relation : that relates words to types. In simple pregroup grammars, typing is a function that maps words to only one type each.

Examples

Some simple, intuitive examples using English as the language to model demonstrate the core principles behind pregroups and their use in linguistic domains.

Let L = {John, Mary, the, dog, cat, met, barked, at}, let T = {N, S, N₀}, and let the following typing relation holds:

John : N Mary : N the : N ⋅ N 0 l dog : N 0 cat : N 0 met : N r ⋅ S ⋅ N l barked : N r ⋅ S at : S r ⋅ N r r ⋅ N r ⋅ S ⋅ N l

A sentence S that has type T is said to be grammatical if T ≤ S . We can prove this by use of a chain of ≤ . For example, we can prove that John met Mary : N ⋅ N r ⋅ S ⋅ N l ⋅ N is grammatical by proving that N ⋅ N r ⋅ S ⋅ N l ⋅ N ≤ S :

N ⋅ N r ⋅ S ⋅ N l ⋅ N ≤ S ⋅ N l ⋅ N ≤ S

by first using contraction on N ⋅ N r and then again on N l ⋅ N . A more convenient notation exists, however, that indicates contractions by connecting them with a drawn link between the contracting types (provided that the links are nested, i.e. don't cross). Words are also typically placed above their types to make the proof more intuitive. The same proof in this notation is simply

A more complex example proves that the dog barked at the cat is grammatical:

Semantics of pregroup grammars

Because of the lack of function types in PG, the usual method of giving a semantics via the λ-calculus or via function denotations is not available in any obvious way. Instead, two different methods exist, one purely formal method that corresponds to the λ-calculus, and one denotational method analogous to (a fragment of) the tensor mathematics of quantum mechanics.

Purely formal semantics

The purely formal semantics for PG consists of a logical language defined according to the following rules:

Given a set of atomic terms T = {a, b, ...} and atomic function symbols F = {f_m, g_n, ...} (where subscripts are meta-notational indicating arity), and variables x, y, ..., all constants, variables, and well-formed function applications are basic terms (a function application is well-formed when the function symbol is applied to the appropriate number of arguments, which can be drawn from the atomic terms, variables, or can be other basic terms)

Any basic term is a term

Given any variable x, [x] is a term

Given any terms m and n, m ⋅ n is a term

Some examples of terms are f(x), g(a,h(x,y)), g ( x , b ) ⋅ [ x ] . A variable x is free in a term t if [x] does not appear in t, and a term with no free variables is a closed term. Terms can be typed with pregroup types in the obvious manner.

The usual conventions regarding α conversion apply.

For a given language, we give an assignment I that maps typed words to typed closed terms in a way that respects the pregroup structure of the types. For the English fragment given above we might therefore have the following assignment (with the obvious, implicit set of atomic terms and function symbols):

I ( J o h n : N ) = j : E I ( M a r y : N ) = m : E I ( t h e : N ⋅ N 0 l ) = ι ( p ) ⋅ [ p ] : E ⋅ E 0 l I ( d o g : N 0 ) = d o g : E 0 I ( c a t : N 0 ) = c a t : E 0 I ( m e t : N r ⋅ S ⋅ N l ) = [ x ] ⋅ m e t ( x , y ) ⋅ [ y ] : E r ⋅ T ⋅ E l I ( b a r k e d : N r ⋅ S ) = [ x ] ⋅ b a r k e d ( x ) : E r ⋅ T I ( a t : S r ⋅ N r r ⋅ N r ⋅ S ⋅ N l ) = [ x ] ⋅ y ⋅ [ y ] ⋅ a t ( x , z ) ⋅ [ z ] : T r ⋅ E r r ⋅ E r ⋅ T ⋅ E l

where E is the type of entities in the domain, and T is the type of truth values.

Together with this core definition of the semantics of PG, we also have a reduction rules that are employed in parallel with the type reductions. Placing the syntactic types at the top and semantics below, we have

For example, applying this to the types and semantics for the sentence John met Mary : N ⋅ ( N r ⋅ S ⋅ N l ) ⋅ N (emphasizing the link being reduced)

For the sentence the dog barked at the cat : ( N ⋅ N 0 l ) ⋅ N 0 ⋅ ( N r ⋅ S ) ⋅ ( S r ⋅ N r r ⋅ N r ⋅ S ⋅ N l ) ⋅ ( N ⋅ N 0 l ) ⋅ N 0 :

References

Pregroup grammar Wikipedia

(Text) CC BY-SA