Samiksha Jaiswal (Editor)

Polytropic process

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Polytropic process

A polytropic process is a thermodynamic process that obeys the relation:

Contents

p v n = C

where p is the pressure, v is specific volume, n is the polytropic index (a real number), and C is a constant. The polytropic process equation can describe multiple expansion and compression processes which include heat transfer.

If the ideal gas law applies, a process is polytropic if and only if the ratio (K) of energy transfer as heat to energy transfer as work at each infinitesimal step of the process is kept constant:

K = δ Q δ W = constant

Particular cases

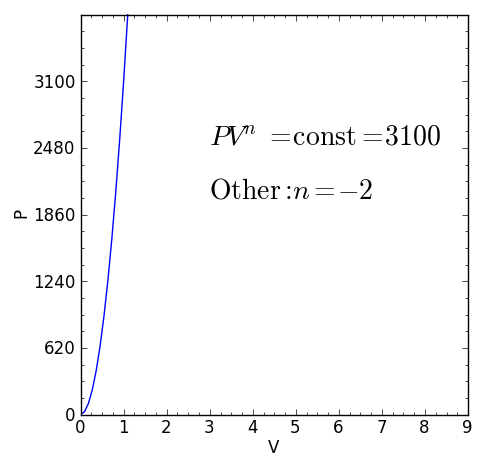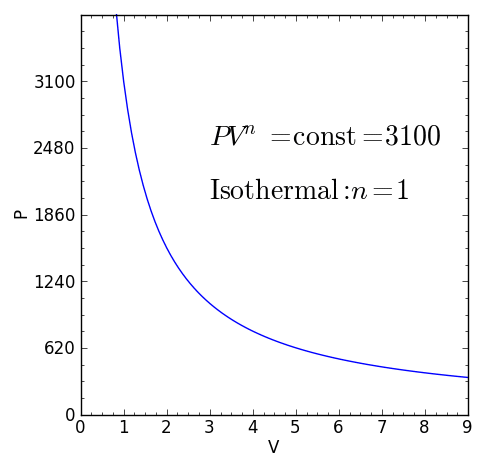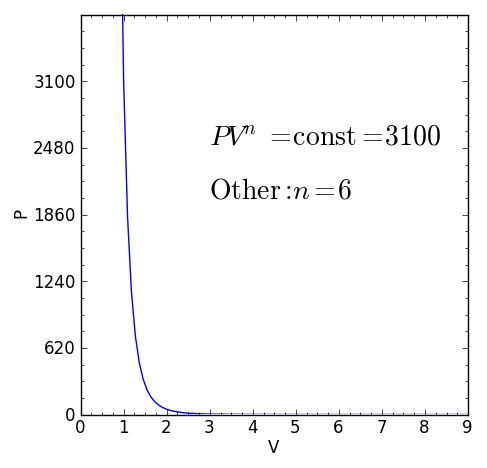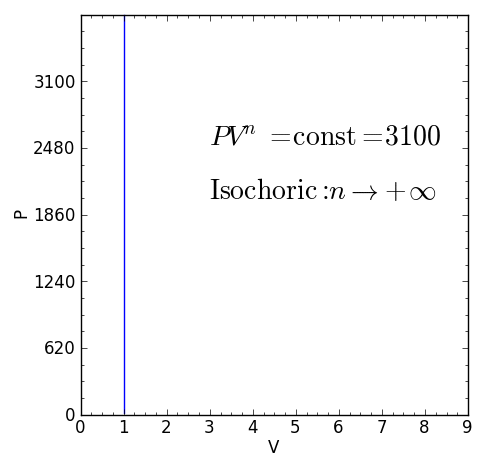
Some specific values of n correspond to particular cases:

  • n = 0 is an isobaric process,
  • n = + ∞ is an isochoric process.

    • In addition, when the ideal gas law applies:

  • n = 1 is an isothermic process,
  • n = γ is an adiabatic process.

    • Equivalence between the polytropic coefficient and the ratio of energy transfers

    Consider an ideal gas in a closed system undergoing a slow process with negligible changes in kinetic and potential energy. For an infinitesimal step of time, the first law of thermodynamics states that the energy added to a system as heat δq, minus the energy that leaves the system as work δw, is equal to the change in the internal energy du of the system:

    δ q − δ w = d u         (Eq. 1)

    Define the energy transfer ratio,

    K = δ q δ w or δ q = K δ w .

    Transfer of work to the environment can be expressed as δ w = p d v and internal energy change as d u = n c v d T

    By substituting the above expressions for δw and δq into the first law:

    ( K − 1 ) p d v = n c v d T         (Eq. 1)

    Writing the ideal gas law in differential form

    p d v + v d p = n R d T → v d p p d v + 1 = n R d T p d v = n R ( K − 1 ) p d T p n c v d T = R ( K − 1 ) c v

    By Mayer's relation, this becomes:

    v d p p d v = ( c p − c v ) ( K − 1 ) c v − 1 = ( K − 1 ) γ − K ⟶ d p p + ( ( 1 − γ ) K + γ ) d v v = 0

    where γ is the heat capacity ratio. Assuming K (and γ) remain constant during the transformation, as d f f = d ( l o g f ) this relation can be integrated as

    d ( l o g p + ( ( 1 − γ ) K + γ ) l o g v ) = 0 ⟶ p v ( 1 − γ ) K + γ = C

    where C is a constant.

    Thus, the process is polytropic, with the coefficient n = ( 1 − γ ) K + γ .

    This derivation can be expanded to include polytropic processes in open systems, including instances where the kinetic energy (i.e. Mach number) is significant. It can also be expanded to include irreversible polytropic processes.

    Relationship to ideal processes

    For certain values of the polytropic index, the process will be synonymous with other common processes. Some examples of the effects of varying index values are given in the table.

    When the index n is between any two of the former values (0, 1, γ, or ∞), it means that the polytropic curve will cut through (be bounded by) the curves of the two bounding indices.

    For an ideal gas, 1 < γ < 2, since by Mayer's relation

    γ = c p c v = c v + R c v = 1 + R c v = c p c p − R .

    Other

    A solution to the Lane–Emden equation using a polytropic fluid is known as a polytrope.

    References

    Polytropic process Wikipedia
    (Text) CC BY-SA