Phase qubit

Introduction

A phase qubit is a current-biased Josephson junction, operated in the zero voltage state with a non-zero current bias.

A Josephson junction is a tunnel junction, made of two pieces of superconducting metal separated by a very thin insulating barrier, about 1 nm in thickness. The barrier is thin enough that electrons, or in the superconducting state, Cooper-paired electrons, can tunnel through the barrier at an appreciable rate. Each of the superconductors that make up the Josephson junction is described by a macroscopic wavefunction, as described by the Ginzburg-Landau theory for superconductors. The difference in the complex phases of the two superconducting wavefunctions is the most important dynamic variable for the Josephson junction, and is called the phase difference δ , or simply "phase".

Main equations describing the SIS junction

The Josephson equation relates the superconducting current (usually called the supercurrent) I through the tunnel junction to the phase difference δ ,

I = I 0 sin ⁡ δ (Josephson current-phase relationship)

Here I 0 is the critical current of the tunnel junction, determined by the area and thickness of the tunnel barrier in the junction, and by the properties of the superconductors on either side of the barrier. For a junction with identical superconductors on either side of the barrier, the critical current is related to the superconducting gap Δ and the normal state resistance R n of the tunnel junction by the Ambegaokar-Baratoff formula

I 0 = π Δ 2 e R n (Ambegaokar-Baratoff formula)

The Gor'kov phase evolution equation gives the rate of change of the phase (the "velocity" of the phase) as a linear function of the voltage V as

V = ℏ 2 e d δ d t (Gor'kov-Josephson phase evolution equation)

This equation is a generalization of the Schrödinger equation for the phase of the BCS wavefunction. The generalization was carried out by Gor'kov in 1958.

The McCumber-Stewart model

The alternative and direct current Josephson relations control the behavior of the Josephson junction itself. The geometry of the Josephson junction—two plates of superconducting metal separated by a thin tunnel barrier—is that of a parallel plate capacitor, so in addition to the Josephson element the device includes a parallel capacitance C . The external circuit is usually simply modeled as a resistor R in parallel with the Josephson element. The set of three parallel circuit elements is biased by an external current source I , thus the current-biased Josephson junction. Solving the circuit equations yields a single dynamic equation for the phase,

ℏ C 2 e d 2 δ d t 2 + ℏ 2 e R d δ d t = I − I 0 sin ⁡ δ .

The terms on the left side are identical to those of a particle with coordinate (location) δ , with mass proportional to the capacitance C , and with friction inversely proportional to the resistance R . The particle moves in a conservative force field given by the term on the right, which corresponds to the particle interacting with a potential energy U ( δ ) given by

U ( δ ) = ℏ 2 e ( − I 0 cos ⁡ δ − I δ ) .

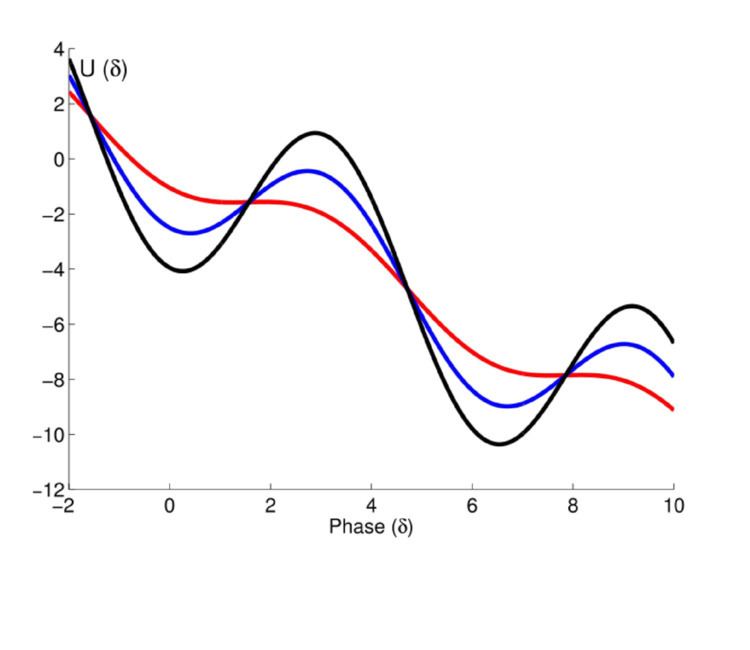
This is the "washboard potential", so-called because it has an overall linear dependence − I δ , modulated by the washboard modulation − I 0 cos ⁡ δ .

The zero voltage state describes one of the two distinct dynamic behaviors displayed by the phase particle, and corresponds to when the particle is trapped in one of the local minima in the washboard potential. These minima exist for bias currents | I | < I 0 , i.e. for currents below the critical current. With the phase particle trapped in a minimum, it has zero average velocity and therefore zero average voltage. A Josephson junction will allow currents up to I 0 to pass through without any voltage; this corresponds to the superconducting branch of the Josephson junction's current-voltage characteristic.

The voltage state is the other dynamic behavior displayed by a Josephson junction, and corresponds to the phase particle free-running down the slope of the potential, with a non-zero average velocity and therefore non-zero voltage. This behavior always occurs for currents I above the critical current, i.e. for | I | > I 0 , and for large resistances R also occurs for currents somewhat below the critical current. This state corresponds to the voltage branch of the Josephson junction current-voltage characteristic. For large resistance junctions the zero-voltage and voltage branches overlap for some range of currents below the critical current, so the device behavior is hysteretic.

Nonlinear inductor

Another way to understand the behavior of a Josephson junction in the zero-voltage state is to consider the SIS tunnel junction as a nonlinear inductor. When the phase is trapped in one of the minima, the phase value is limited to a small range about the phase value at the potential minimum, which we will call δ 0 . The current through the junction is related to this phase value by

I = I 0 sin ⁡ δ 0 .

If we consider small variations Δ δ in the phase about the minimum δ 0 (small enough to maintain the junction in the zero voltage state), then the current will vary by

Δ I = ( I 0 cos ⁡ δ 0 ) Δ δ .

These variations in the phase give rise to a voltage through the ac Josephson relation,

Δ V = ℏ 2 e d Δ δ d t = ℏ 2 e 1 I 0 cos ⁡ δ 0 d Δ I d t = L d Δ I d t

This last relation is the defining equation for an inductor with inductance

L = ℏ 2 e 1 I 0 cos ⁡ δ 0 .

This inductance depends on the value of phase δ 0 at the minimum in the washboard potential, so the inductance value can be controlled by changing the bias current I . For zero bias current, the inductance reaches its minimum value,

L m i n = ℏ 2 e 1 I 0 = ℏ R n π Δ .

As the bias current increases, the inductance increases. When the bias current is very close (but less than) the critical current I 0 , the value of the phase δ 0 is very close to π / 2 , as seen by the dc Josephson relation, above. This means that the inductance value L becomes very large, diverging as I reaches the critical current I 0 .

The nonlinear inductor represents the response of the Josephson junction to changes in bias current. When the parallel capacitance from the device geometry is included, in parallel with the inductor, this forms a nonlinear L C resonator, with resonance frequency

ω p = 1 L C = 2 e I 0 cos ⁡ δ 0 ℏ C ,

which is known as the plasma frequency of the junction. This corresponds to the oscillation frequency of the phase particle in the bottom of one of the minima of the washboard potential.

For bias currents very near the critical current, the phase value in the washboard minimum is

cos ⁡ δ 0 = 1 − ( I / I 0 ) 2 ,

and the plasma frequency is then

ω p ≈ 2 e I 0 ℏ C [ 1 − ( I / I 0 ) 2 ] 1 / 4 ,

clearly showing that the plasma frequency approaches zero as the bias current approaches the critical current.

The simple tunability of the current-biased Josephson junction in its zero voltage state is one of the key advantages the phase qubit has over some other qubit implementations, although it also limits the performance of this device, as fluctuations in current generate fluctuations in the plasma frequency, which causes dephasing of the quantum states.

Quantized energy levels

The phase qubit is operated in the zero-voltage state, with | I | < I 0 . At very low temperatures, much less than 1 K (achievable using a cryogenic system known as a dilution refrigerator), with a sufficiently high resistance and small capacitance Josephson junction, quantum energy levels become detectable in the local minima of the washboard potential. These were first detected using microwave spectroscopy, where a weak microwave signal is added to the current I biasing the junction. Transitions from the zero voltage state to the voltage state were measured by monitoring the voltage across the junction. Clear resonances at certain frequencies were observed, which corresponded well with the quantum transition energies obtained by solving the Schrödinger equation for the local minimum in the washboard potential. Classically only a single resonance is expected, centered at the plasma frequency ω p . Quantum mechanically, the potential minimum in the washboard potential can accommodate several quantized energy levels, with the lowest (ground to first excited state) transition at an energy E 01 ≈ ℏ ω p , but the higher energy transitions (first to second excited state, second to third excited state) shifted somewhat below this due to the non-harmonic nature of the trapping potential minimum, whose resonance frequency falls as the energy increases in the minimum. Observing multiple, discrete levels in this fashion is extremely strong evidence that the superconducting device is behaving quantum mechanically, rather than classically.

The phase qubit uses the lowest two energy levels in the local minimum; the ground state | g ⟩ is the "zero state" of the qubit, and the first excited state | e ⟩ is the "one state". The slope in the washboard potential is set by the bias current I , and changes in this current change the washboard potential, changing the shape of the local minimum (equivalently, changing the value of the nonlinear inductance, as discussed above). This changes the energy difference between the ground and first excited states. Hence the phase qubit has a tunable energy splitting.