Type JohnsonJ5 - J6 - J7 Vertices 20 | Edges 35 Symmetry group C5v | |
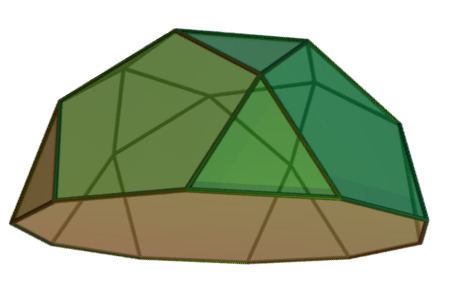 | ||
Vertex configuration 2.5(3.5.3.5)10(3.5.10) | ||
In geometry, the pentagonal rotunda is one of the Johnson solids (J6). It can be seen as half an icosidodecahedron.
Contents
A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
Formulae
The following formulae for volume, surface area, circumradius and height can be used if all faces are regular, with edge length a:
Dual polyhedron
The dual of the pentagonal rotunda has 20 faces: 10 triangular, 5 rhombic, and 5 kites.
