Padovan sequence

Recurrence relations

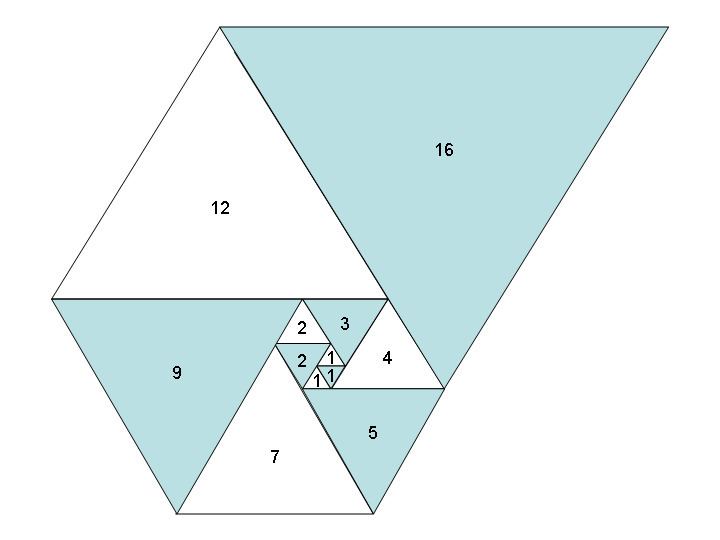
In the spiral, each triangle shares a side with two others giving a visual proof that the Padovan sequence also satisfies the recurrence relation

P ( n ) = P ( n − 1 ) + P ( n − 5 )

Starting from this, the defining recurrence and other recurrences as they are discovered, one can create an infinite number of further recurrences by repeatedly replacing P ( m ) by P ( m − 2 ) + P ( m − 3 )

The Perrin sequence satisfies the same recurrence relations as the Padovan sequence, although it has different initial values. This is a property of recurrence relations.

The Perrin sequence can be obtained from the Padovan sequence by the following formula:

P e r r i n ( n ) = P ( n + 1 ) + P ( n − 10 ) .

Extension to negative parameters

As with any sequence defined by a recurrence relation, Padovan numbers P(m) for m<0 can be defined by rewriting the recurrence relation as

P ( m ) = P ( m + 3 ) − P ( m + 1 ) ,

Starting with m = −1 and working backwards, we extend P(m) to negative indices:

Sums of terms

The sum of the first n terms in the Padovan sequence is 2 less than P(n + 5) i.e.

∑ m = 0 n P ( m ) = P ( n + 5 ) − 2.

Sums of alternate terms, sums of every third term and sums of every fifth term are also related to other terms in the sequence:

∑ m = 0 n P ( 2 m ) = P ( 2 n + 3 ) − 1  A077855 ∑ m = 0 n P ( 2 m + 1 ) = P ( 2 n + 4 ) − 1 ∑ m = 0 n P ( 3 m ) = P ( 3 n + 2 )  A034943 ∑ m = 0 n P ( 3 m + 1 ) = P ( 3 n + 3 ) − 1 ∑ m = 0 n P ( 3 m + 2 ) = P ( 3 n + 4 ) − 1 ∑ m = 0 n P ( 5 m ) = P ( 5 n + 1 ) .  A012772

Sums involving products of terms in the Padovan sequence satisfy the following identities:

∑ m = 0 n P ( m ) 2 = P ( n + 2 ) 2 − P ( n − 1 ) 2 − P ( n − 3 ) 2 ∑ m = 0 n P ( m ) 2 P ( m + 1 ) = P ( n ) P ( n + 1 ) P ( n + 2 ) ∑ m = 0 n P ( m ) P ( m + 2 ) = P ( n + 2 ) P ( n + 3 ) − 1.

Other identities

The Padovan sequence also satisfies the identity

P ( n ) 2 − P ( n + 1 ) P ( n − 1 ) = P ( − n − 7 ) .

The Padovan sequence is related to sums of binomial coefficients by the following identity:

P ( k − 2 ) = ∑ 2 m + n = k ( m n ) = ∑ m = ⌈ k / 3 ⌉ ⌊ k / 2 ⌋ ( m k − 2 m ) .

For example, for k = 12, the values for the pair (m, n) with 2m + n = 12 which give non-zero binomial coefficients are (6, 0), (5, 2) and (4, 4), and:

( 6 0 ) + ( 5 2 ) + ( 4 4 ) = 1 + 10 + 1 = 12 = P ( 10 ) .

Binet-like formula

The Padovan sequence numbers can be written in terms of powers of the roots of the equation

x 3 − x − 1 = 0.

This equation has 3 roots; one real root p (known as the plastic number) and two complex conjugate roots q and r. Given these three roots, the Padovan sequence can be expressed by a formula involving p,q and r:

P ( n ) = a p n + b q n + c r n

where a, b and c are constants.

Since the magnitudes of the complex roots q and r are both less than 1 (and hence p is a Pisot–Vijayaraghavan number), the powers of these roots approach 0 for large n, and P ( n ) − a p n tends to zero.

For all n ≥ 0 , P(n) is the integer closest to p n − 1 s , where s = p/a = 1.0453567932525329623... is the only real root of s³ − 2s² + 23s − 23 = 0. The ratio of successive terms in the Padovan sequence approaches p, which has a value of approximately 1.324718. This constant bears the same relationship to the Padovan sequence and the Perrin sequence as the golden ratio does to the Fibonacci sequence.

Combinatorial interpretations

P(n) is the number of ways of writing n + 2 as an ordered sum in which each term is either 2 or 3 (i.e. the number of compositions of n + 2 in which each term is either 2 or 3). For example, P(6) = 4, and there are 4 ways to write 8 as an ordered sum of 2s and 3s:

The number of ways of writing n as an ordered sum in which no term is 2 is P(2n − 2). For example, P(6) = 4, and there are 4 ways to write 4 as an ordered sum in which no term is 2:

The number of ways of writing n as a palindromic ordered sum in which no term is 2 is P(n). For example, P(6) = 4, and there are 4 ways to write 6 as a palindromic ordered sum in which no term is 2:

The number of ways of writing n as an ordered sum in which each term is odd and greater than 1 is equal to P(n − 5). For example, P(6) = 4, and there are 4 ways to write 11 as an ordered sum in which each term is odd and greater than 1:

The number of ways of writing n as an ordered sum in which each term is congruent to 2 mod 3 is equal to P(n − 4). For example, P(6) = 4, and there are 4 ways to write 10 as an ordered sum in which each term is congruent to 2 mod 3:

Generating function

The generating function of the Padovan sequence is

G ( P ( n ) ; x ) = 1 + x 1 − x 2 − x 3 .

This can be used to prove identities involving products of the Padovan sequence with geometric terms, such as:

∑ n = 0 ∞ P ( n ) 2 n = 12 5 . ∑ n = 0 ∞ P ( n ) α n = α 2 ( α + 1 ) α 3 − α − 1 .

Generalizations

In a similar way to the Fibonacci numbers that can be generalized to a set of polynomials called the Fibonacci polynomials, the Padovan sequence numbers can be generalized to yield the Padovan polynomials.

Padovan prime

A Padovan prime is P(n) that is prime. The first few Padovan primes are

2, 3, 5, 7, 37, 151, 3329, 23833, .... (sequence A100891 in the OEIS)

Padovan L-system

If we define the following simple grammar:

variables : A B Cconstants : nonestart  : Arules  : (A → B), (B → C), (C → AB)

then this Lindenmayer system or L-system produces the following sequence of strings:

n = 0 : An = 1 : Bn = 2 : Cn = 3 : ABn = 4 : BCn = 5 : CABn = 6 : ABBCn = 7 : BCCABn = 8 : CABABBC

and if we count the length of each string, we obtain the Padovan sequence of numbers:

1 1 1 2 2 3 4 5 ...

Also, if you count the number of As, Bs and Cs in each string, then for the nth string, you have P(n − 5) As, P(n − 3) Bs and P(n − 4) Cs. The count of BB pairs, AA pairs and CC pairs are also Padovan numbers.

Cuboid spiral

A spiral can be formed based on connecting the corners of a set of 3-dimensional cuboids. This is the Padovan cuboid spiral. Successive sides of this spiral have lengths that are the Padovan sequence numbers multiplied by the square root of 2.

Pascal's Triangle

Erv Wilson in his paper The Scales of Mt. Meru discovered the Padovan sequence in Pascal's Triangle by summing the diagonal numbers (see diagram). Correction, Erv Wilson noticed these diagonals and drew them on paper in 1993, yet the Padovan numbers were not discovered until 1994. Tony Foster (2016) actually defined these diagonals as being related to the Padovan sequence. Below is his chart.