 | ||
In optics, various autocorrelation functions can be experimentally realized. The field autocorrelation may be used to calculate the spectrum of a source of light, while the intensity autocorrelation and the interferometric autocorrelation are commonly used to estimate the duration of ultrashort pulses produced by modelocked lasers. The laser pulse duration cannot be easily measured by optoelectronic methods, since the response time of photodiodes and oscilloscopes are at best of the order of 200 femtoseconds, yet laser pulses can be made as short as a few femtoseconds.
Contents
- Field autocorrelation
- Intensity autocorrelation
- Interferometric autocorrelation
- Pupil function autocorrelation
- References
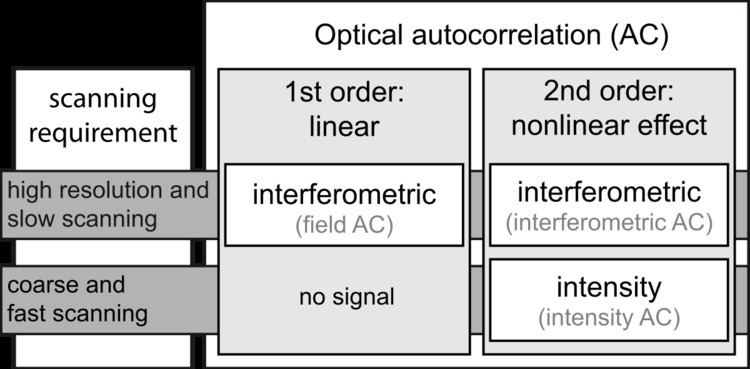
In the following examples, the autocorrelation signal is generated by the nonlinear process of second-harmonic generation (SHG). Other techniques based on two-photon absorption may also be used in autocorrelation measurements, as well as higher-order nonlinear optical processes such as third-harmonic generation, in which case the mathematical expressions of the signal will be slightly modified, but the basic interpretation of an autocorrelation trace remains the same. A detailed discussion on interferometric autocorrelation is given in several well-known textbooks.
Field autocorrelation
For a complex electric field
The Wiener-Khinchin theorem states that the Fourier transform of the field autocorrelation is the spectrum of
The field autocorrelation is readily measured experimentally by placing a slow detector at the output of a Michelson interferometer. The detector is illuminated by the input electric field
Expanding
Intensity autocorrelation
To a complex electric field
The optical implementation of the intensity autocorrelation is not as straightforward as for the field autocorrelation. Similarly to the previous setup, two parallel beams with a variable delay are generated, then focused into a second-harmonic-generation crystal (see nonlinear optics) to obtain a signal proportional to
The generation of the second harmonic in crystals is a nonlinear process that requires high peak power, unlike the previous setup. However, such high peak power can be obtained from a limited amount of energy by ultrashort pulses, and as a result their intensity autocorrelation is often measured experimentally. Another difficulty with this setup is that both beams must be focused at the same point inside the crystal as the delay is scanned in order for the second harmonic to be generated.
It can be shown that the intensity autocorrelation width of a pulse is related to the intensity width. For a Gaussian time profile, the autocorrelation width is
Interferometric autocorrelation
As a combination of both previous cases, a nonlinear crystal can be used to generate the second harmonic at the output of a Michelson interferometer, in a collinear geometry. In this case, the signal recorded by a slow detector is
Pupil function autocorrelation
The optical transfer function T(w) of an optical system is given by the autocorrelation of its pupil function f(x,y):
