 | ||
Bauer 1
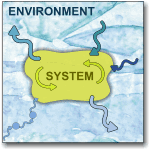
In physics, an open quantum system is a quantum-mechanical system which interacts with an external quantum system, the environment. In reality, no quantum system is completely isolated from its surroundings, thus quantum system is open to some extent, causing dissipation in the quantum system. Techniques developed in the context of open quantum systems have proven powerful in fields such as quantum optics, quantum measurement theory, quantum statistical mechanics, quantum information science, quantum thermodynamics, quantum cosmology and semi-classical approximations.
Contents
- Bauer 1
- Introduction to the lecture series
- Quantum system and environment
- Open quantum system dynamics
- References
Introduction to the lecture series
Quantum system and environment
No quantum system can be completely isolated from its environment. As a direct result a quantum system is never be a pure state. A pure state is unitary equivalent to a zero temperature ground state forbidden by the third law of thermodynamics. A complete description of a quantum system requires to include the environment. The outcome of this process of embedding is that ultimately we end with the state of whole universe described by a wavefunction
Even if the combined system is pure state and can be described by a wavefunction
Open quantum system dynamics
The theory of open quantum systems seeks an economical treatment of the dynamics of observables that can be associated with the system. Typical observables are energy and quantum coherence. Loss of energy to the environment is termed quantum dissipation. Loss of coherence is termed quantum decoherence. The environment we wish to model as part of our open quantum system is typically very large, making exact solutions impossible to calculate. The reduction problem is difficult therefore a diversity of approaches have been pursued. A common objective is to derive a reduced description where the system's dynamics is considered explicitly and the bath is described implicitly.
The main assumption is that the entire world is a large closed system, and therefore, time evolution is governed by a unitary transformation generated by a global Hamiltonian. For the combined system bath scenario the global Hamiltonian can be decomposed into:
where
When the interaction between the system and the environment is weak a time dependent perturbation theory seems appropriate. The typical assumption is that the system and bath are initially uncorrelated
An alternative derivation employing projection operator techniques is known as the Nakajima–Zwanzig equation. The derivation highlight the problem that the reduced dynamics is non-local in time:
The effect of the bath is hidden in the momrey kernel
Another approach emerges as an analogue of classical dissipation theory developed by Ryogo Kubo and Y. Tanimura. This approach is connected to Hierarchical equations of motion which embed the density operator in a larger space of auxiliary operators such that a time local equation is obtained for the whole set and their memory is contained in the auxiliary operators.
A formal construction of a local equation of motion with a Markovian property is an alternative to a reduced derivation. The theory is based on an axiomatic approach. The basic starting point is a completely positive map. The assumption is that the initial system-environment state is uncorrelated
is the dissipative part describing implicitly through system operators
In 1981, Amir Caldeira and Anthony J. Leggett proposed a simplifying assumption in which the bath is decomposed to normal modes represented as harmonic oscillators linearly coupled to the system. As a result the influence of the bath can be summarized by the bath spectral function. This method is known as the Caldeira–Leggett or harmonic bath model. To proceed and obtain explicit solutions, typically the path integral formulation description of quantum mechanics is employed.
The harmonic normal-mode bath leads to a physically consistent picture of quantum dissipation. Nevertheless its ergodic properties are too weak. The dynamics does not generate wide scale quantum entanglement between the bath modes.
An alternative bath model is a spin bath. At low temperature and weak system-bath coupling these two bath models are equivalent. But for higher excitation the spin bath has strong ergodic properties. Once the system is coupled significant entanglement is generated between all modes. A spin bath can simulate a harmonic bath but the opposite is not true.
A natural system coupled to a spin bath is an N-V center in diamond. The color center is the system and the bath consists of 13C impurities which interact with the system via magnetic dipole-dipole interaction.
