In numerical analysis, a branch of applied mathematics, the midpoint method is a one-step method for numerically solving the differential equation,
y ′ ( t ) = f ( t , y ( t ) ) , y ( t 0 ) = y 0 .
The explicit midpoint method is given by the formula
y n + 1 = y n + h f ( t n + h 2 , y n + h 2 f ( t n , y n ) ) , ( 1 e ) the implicit midpoint method by
y n + 1 = y n + h f ( t n + h 2 , 1 2 ( y n + y n + 1 ) ) , ( 1 i ) for n = 0 , 1 , 2 , … Here, h is the step size — a small positive number, t n = t 0 + n h , and y n is the computed approximate value of y ( t n ) . The explicit midpoint method is also known as the modified Euler method, the implicit method is the most simple collocation method, and, applied to Hamiltionian dynamics, a symplectic integrator.
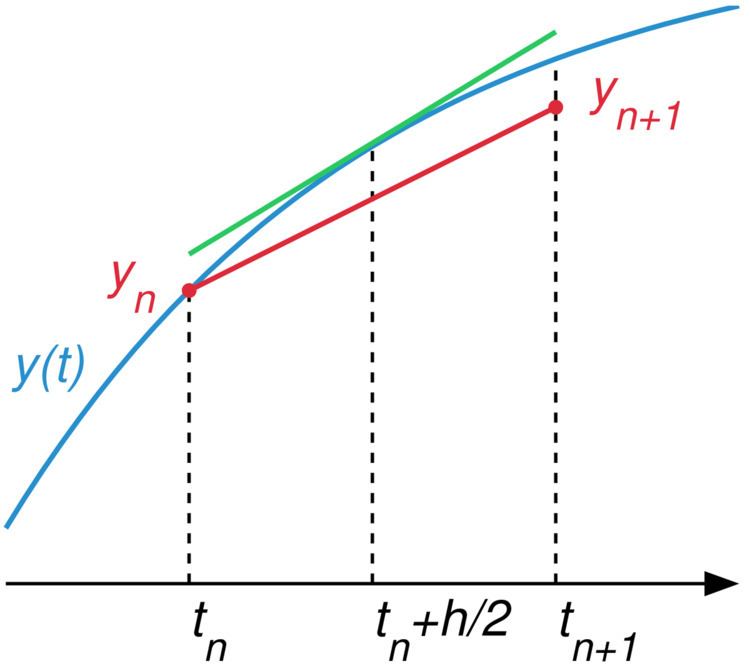
The name of the method comes from the fact that in the formula above the function f giving the slope of the solution is evaluated at t = t n + h / 2 , (note : t is t n + t n + 1 2 ) which is the midpoint between t n at which the value of y(t) is known and t n + 1 at which the value of y(t) needs to be found.
The local error at each step of the midpoint method is of order O ( h 3 ) , giving a global error of order O ( h 2 ) . Thus, while more computationally intensive than Euler's method, the midpoint method's error generally decreases faster as h → 0 .
The methods are examples of a class of higher-order methods known as Runge-Kutta methods.
The midpoint method is a refinement of the Euler's method
y n + 1 = y n + h f ( t n , y n ) , and is derived in a similar manner. The key to deriving Euler's method is the approximate equality
y ( t + h ) ≈ y ( t ) + h f ( t , y ( t ) ) ( 2 ) which is obtained from the slope formula
y ′ ( t ) ≈ y ( t + h ) − y ( t ) h ( 3 ) and keeping in mind that y ′ = f ( t , y ) .
For the midpoint methods, one replaces (3) with the more accurate
y ′ ( t + h 2 ) ≈ y ( t + h ) − y ( t ) h when instead of (2) we find
y ( t + h ) ≈ y ( t ) + h f ( t + h 2 , y ( t + h 2 ) ) . ( 4 ) One cannot use this equation to find y ( t + h ) as one does not know y at t + h / 2 . The solution is then to use a Taylor series expansion exactly as if using the Euler method to solve for y ( t + h / 2 ) :
y ( t + h 2 ) ≈ y ( t ) + h 2 y ′ ( t ) = y ( t ) + h 2 f ( t , y ( t ) ) , which, when plugged in (4), gives us
y ( t + h ) ≈ y ( t ) + h f ( t + h 2 , y ( t ) + h 2 f ( t , y ( t ) ) ) and the explicit midpoint method (1e).
The implicit method (1i) is obtained by approximating the value at the half step t + h / 2 by the midpoint of the line segment from y ( t ) to y ( t + h )
y ( t + h 2 ) ≈ 1 2 ( y ( t ) + y ( t + h ) ) and thus
y ( t + h ) − y ( t ) h ≈ y ′ ( t + h 2 ) ≈ k = f ( t + h 2 , 1 2 ( y ( t ) + y ( t + h ) ) ) Inserting the approximation y n + h k for y ( t n + h ) results in the implicit Runge-Kutta method
k = f ( t n + h 2 , y n + h 2 k ) y n + 1 = y n + h k which contains the implicit Euler method with step size h / 2 as its first part.
Because of the time symmetry of the implicit method, all terms of even degree in h of the local error cancel, so that the local error is automatically of order O ( h 3 ) . Replacing the implicit with the explicit Euler method in the determination of k results again in the explicit midpoint method.