Michaelis–Menten kinetics

Model

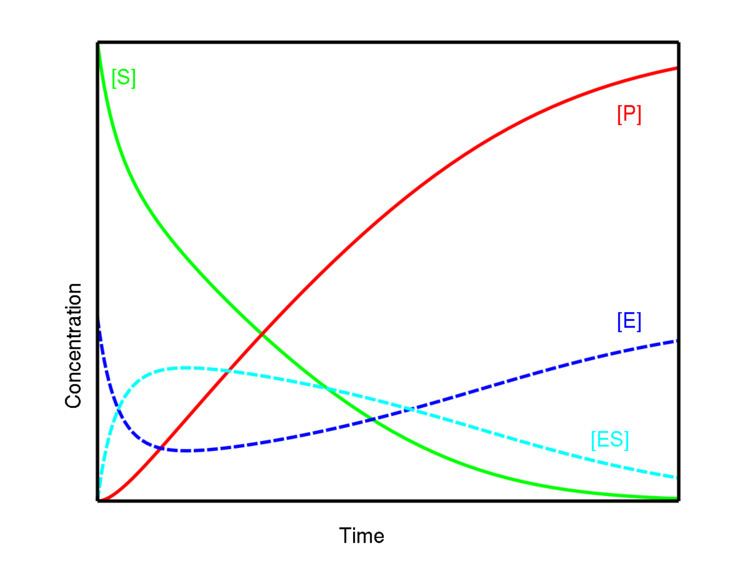
In 1903, French physical chemist Victor Henri found that enzyme reactions were initiated by a bond (more generally, a binding interaction) between the enzyme and the substrate. His work was taken up by German biochemist Leonor Michaelis and Canadian physician Maud Menten, who investigated the kinetics of an enzymatic reaction mechanism, invertase, that catalyzes the hydrolysis of sucrose into glucose and fructose. In 1913, they proposed a mathematical model of the reaction. It involves an enzyme, E, binding to a substrate, S, to form a complex, ES, which in turn releases a product, P, regenerating the original enzyme. This may be represented schematically as

E + S ⇌ k r k f ES → k cat E + P

where k f (forward rate), k r (reverse rate), and k c a t (catalytic rate) denote the rate constants, the double arrows between S (substrate) and ES (enzyme-substrate complex) represent the fact that enzyme-substrate binding is a reversible process, and the single forward arrow represents the formation of P (product).

Under certain assumptions – such as the enzyme concentration being much less than the substrate concentration – the rate of product formation is given by

v = d [ P ] d t = V max [ S ] K M + [ S ] = k c a t [ E ] 0 [ S ] K M + [ S ] .

The reaction order depends on the relative size of the two terms in the denominator. At low substrate concentration [ S ] ≪ K M so that v = k c a t [ E ] 0 [ S ] K M . Under these conditions the reaction rate varies linearly with substrate concentration [ S ] (first-order kinetics). However at higher [ S ] with [ S ] ≫ K M , the reaction becomes independent of [ S ] (zero-order kinetics) and asymptotically approaches its maximum rate V max = k cat [ E ] 0 , where [ E ] 0 is the initial enzyme concentration. This rate is attained when all enzyme is bound to substrate. k c a t , the turnover number, is the maximum number of substrate molecules converted to product per enzyme molecule per second. Further addition of substrate does not increase the rate which is said to be saturated.

The Michaelis constant K M is the [ S ] at which the reaction rate is at half-maximum, and is an inverse measure of the substrate's affinity for the enzyme—as a small K M indicates high affinity, meaning that the rate will approach V max with lower [ S ] than those reactions with a larger K M . The value of K M is dependent on both the enzyme and the substrate, as well as conditions such as temperature and pH.

The model is used in a variety of biochemical situations other than enzyme-substrate interaction, including antigen-antibody binding, DNA-DNA hybridization, and protein-protein interaction. It can be used to characterise a generic biochemical reaction, in the same way that the Langmuir equation can be used to model generic adsorption of biomolecular species. When an empirical equation of this form is applied to microbial growth, it is sometimes called a Monod equation.

Applications

Parameter values vary widely between enzymes:

The constant k cat / K M (catalytic efficiency) is a measure of how efficiently an enzyme converts a substrate into product. Diffusion limited enzymes, such as fumarase, work at the theoretical upper limit of 10⁸ – 10¹⁰ /M*s, limited by diffusion of substrate into the active site.

Michaelis–Menten kinetics have also been applied to a variety of spheres outside of biochemical reactions, including alveolar clearance of dusts, the richness of species pools, clearance of blood alcohol, the photosynthesis-irradiance relationship, and bacterial phage infection.

Derivation

Applying the law of mass action, which states that the rate of a reaction is proportional to the product of the concentrations of the reactants (i.e.[E][S]), gives a system of four non-linear ordinary differential equations that define the rate of change of reactants with time t

d [ E ] d t = − k f [ E ] [ S ] + k r [ E S ] + k c a t [ E S ] d [ S ] d t = − k f [ E ] [ S ] + k r [ E S ] d [ E S ] d t = k f [ E ] [ S ] − k r [ E S ] − k c a t [ E S ] d [ P ] d t = k c a t [ E S ] .

In this mechanism, the enzyme E is a catalyst, which only facilitates the reaction, so that its total concentration, free plus combined, [ E ] + [ E S ] = [ E ] 0 is a constant. This conservation law can also be observed by adding the first and third equations above.

Equilibrium approximation

In their original analysis, Michaelis and Menten assumed that the substrate is in instantaneous chemical equilibrium with the complex, which implies

k f [ E ] [ S ] = k r [ E S ] .

From the enzyme conservation law, we obtain

[ E ] = [ E ] 0 − [ E S ] .

Combining the two expressions above, gives us

k f ( [ E ] 0 − [ E S ] ) [ S ] = k r [ E S ] .

Upon simplification, we get

[ E S ] = [ E ] 0 [ S ] K d + [ S ]

where K d = k r / k f is the dissociation constant for the enzyme-substrate complex. Hence the velocity v of the reaction – the rate at which P is formed – is

v = d [ P ] d t = V max [ S ] K d + [ S ]

where V max = k c a t [ E ] 0 is the maximum reaction velocity.

Quasi-steady-state approximation

An alternative analysis of the system was undertaken by British botanist G. E. Briggs and British geneticist J. B. S. Haldane in 1925. They assumed that the concentration of the intermediate complex does not change on the time-scale of product formation – known as the quasi-steady-state assumption or pseudo-steady-state-hypothesis. Mathematically, this assumption means k f [ E ] [ S ] = k r [ E S ] + k c a t [ E S ] . Combining this relationship with the enzyme conservation law, the concentration of the complex is

[ E S ] = [ E ] 0 [ S ] K M + [ S ]

where

K M = k r + k c a t k f

is known as the Michaelis constant, where k r , k c a t , and k f are, respectively, the constants for substrate unbinding, conversion to product, and binding to the enzyme. Hence the velocity v of the reaction is

v = d [ P ] d t = V max [ S ] K M + [ S ] .

Assumptions and limitations

The first step in the derivation applies the law of mass action, which is reliant on free diffusion. However, in the environment of a living cell where there is a high concentration of proteins, the cytoplasm often behaves more like a gel than a liquid, limiting molecular movements and altering reaction rates. Although the law of mass action can be valid in heterogeneous environments, it is more appropriate to model the cytoplasm as a fractal, in order to capture its limited-mobility kinetics.

The resulting reaction rates predicted by the two approaches are similar, with the only difference being that the equilibrium approximation defines the constant as K d , whilst the quasi-steady-state approximation uses K M . However, each approach is founded upon a different assumption. The Michaelis–Menten equilibrium analysis is valid if the substrate reaches equilibrium on a much faster time-scale than the product is formed or, more precisely, that

ϵ d = k c a t k r ≪ 1 .

By contrast, the Briggs–Haldane quasi-steady-state analysis is valid if

ϵ m = [ E ] 0 [ S ] 0 + K M ≪ 1 .

Thus it holds if the enzyme concentration is much less than the substrate concentration. Even if this is not satisfied, the approximation is valid if K M is large.

In both the Michaelis–Menten and Briggs–Haldane analyses, the quality of the approximation improves as ϵ decreases. However, in model building, Michaelis–Menten kinetics are often invoked without regard to the underlying assumptions.

It is also important to remember that, while irreversibility is a necessary simplification in order to yield a tractable analytic solution, in the general case product formation is not in fact irreversible. The enzyme reaction is more correctly described as

E + S ⇌ k r 1 k f 1 ES ⇌ k r 2 k f 2 E + P .

In general, the assumption of irreversibility is a good one in situations where one of the below is true:

1. The concentration of substrate(s) is very much larger than the concentration of products:

This is true under standard in vitro assay conditions, and is true for many in vivo biological reactions, particularly where the product is continually removed by a subsequent reaction.

2. The energy released in the reaction is very large, that is

In situations where neither of these two conditions hold (that is, the reaction is low energy and a substantial pool of product(s) exists), the Michaelis–Menten equation breaks down, and more complex modelling approaches explicitly taking the forward and reverse reactions into account must be taken to understand the enzyme biology.

Determination of constants

The typical method for determining the constants V max and K M involves running a series of enzyme assays at varying substrate concentrations [ S ] , and measuring the initial reaction rate v 0 . 'Initial' here is taken to mean that the reaction rate is measured after a relatively short time period, during which it is assumed that the enzyme-substrate complex has formed, but that the substrate concentration held approximately constant, and so the equilibrium or quasi-steady-state approximation remain valid. By plotting reaction rate against concentration, and using nonlinear regression of the Michaelis–Menten equation, the parameters may be obtained.

Before computing facilities to perform nonlinear regression became available, graphical methods involving linearisation of the equation were used. A number of these were proposed, including the Eadie–Hofstee diagram, Hanes–Woolf plot and Lineweaver–Burk plot; of these, the Hanes–Woolf plot is the most accurate. However, while useful for visualization, all three methods distort the error structure of the data and are inferior to nonlinear regression. Nonetheless, their use can still be found in modern literature.

In 1997 Santiago Schnell and Claudio Mendoza suggested a closed form solution for the time course kinetics analysis of the Michaelis–Menten kinetics based on the solution of the Lambert W function. Namely:

[ S ] K M = W ( F ( t ) )

where W is the Lambert W function and

F ( t ) = [ S ] 0 K M exp ( [ S ] 0 K M − V max K M t ) .

The above equation has been used to estimate V max and K M from time course data.

Role of substrate unbinding

The Michaelis-Menten equation has been used to predict the rate of product formation in enzymatic reactions for more than a century. Specifically, it states that the rate of an enzymatic reaction will increase as substrate concentration increases, and that increased unbinding of enzyme-substrate complexes will decrease the reaction rate. While the first prediction is well established, the second has never been tested experimentally. To determine whether an increased rate of unbinding does in fact decrease the reaction rate, Shlomi Reuveni et al. mathematically analyzed the effect of enzyme-substrate unbinding on enzymatic reactions at the single-molecule level. According to the study, unbinding of an enzyme from a substrate can reduce the rate of product formation under some conditions, but may also have the opposite effect. As substrate concentrations increase, a tipping point can be reached where an increase in the unbinding rate results in an increase, rather than a decrease, of the reaction rate. The results indicate that enzymatic reactions can behave in ways that violate the classical Michaelis-Menten equation, and that the role of unbinding in enzymatic catalysis still remains to be determined experimentally.