Author of publication Conjectured no. of terms Infinite | Publication year 1536 No. of known terms 49 Subsequence of Mersenne numbers | |
 | ||
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number that can be written in the form Mn = 2n − 1 for some integer n. They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17th century. The first four Mersenne primes (sequence A000668 in the OEIS) are 3, 7, 31, and 127.
Contents
- About Mersenne primes
- Perfect numbers
- History
- Searching for Mersenne primes
- Theorems about Mersenne numbers
- List of known Mersenne primes
- Factorization of composite Mersenne numbers
- Mersenne primitive part
- Mersenne numbers in nature and elsewhere
- MersenneFermat primes
- Generalizations
- Complex numbers
- Gaussian Mersenne primes
- Eisenstein Mersenne primes
- Repunit primes
- Other generalized Mersenne primes
- References
If n is a composite number then so is 2n − 1. (2ab − 1 is divisible by both 2a − 1 and 2b − 1.) The definition is therefore unchanged when written Mp = 2p − 1 where p is assumed prime.
More generally, numbers of the form Mn = 2n − 1 without the primality requirement are called Mersenne numbers. Mersenne numbers are sometimes defined to have the additional requirement that n be prime, equivalently that they be pernicious Mersenne numbers, namely those numbers whose binary representation contains a prime number of ones and no zeros. The smallest composite pernicious Mersenne number is 211 − 1 = 2047 = 23 × 89.
Mersenne primes Mp are also noteworthy due to their connection to perfect numbers.
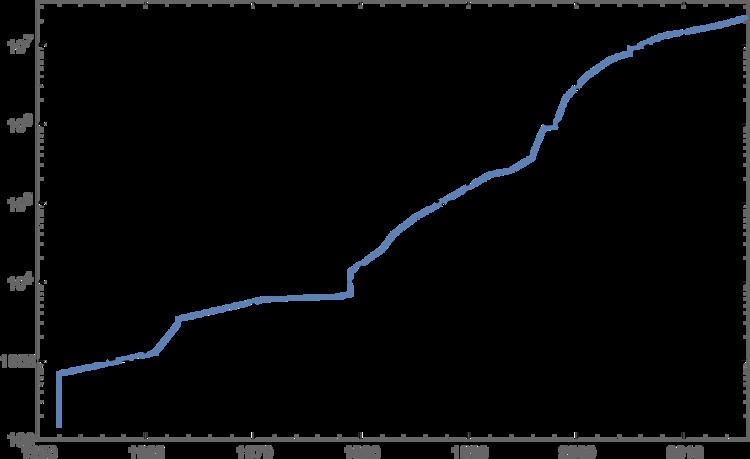
As of January 2016, 49 Mersenne primes are known. The largest known prime number 274,207,281 − 1 is a Mersenne prime.
Since 1997, all newly found Mersenne primes have been discovered by the “Great Internet Mersenne Prime Search” (GIMPS), a distributed computing project on the Internet.
About Mersenne primes
Many fundamental questions about Mersenne primes remain unresolved. It is not even known whether the set of Mersenne primes is finite or infinite. The Lenstra–Pomerance–Wagstaff conjecture asserts that there are infinitely many Mersenne primes and predicts their order of growth. It is also not known whether infinitely many Mersenne numbers with prime exponents are composite, although this would follow from widely believed conjectures about prime numbers, for example, the infinitude of Sophie Germain primes congruent to 3 (mod 4), for these primes p, 2p + 1 (which is also prime) will divide Mp, e.g., 23 | M11, 47 | M23, 167 | M83, 263 | M131, 359 | M179, 383 | M191, 479 | M239, and 503 | M251. (sequence A002515 in the OEIS). Since for these primes p, 2p + 1 is congruent to 7 mod 8, so 2 is a quadratic residue mod 2p + 1, and the multiplicative order of 2 mod 2p + 1 must divide
The first four Mersenne primes are
M2 = 3, M3 = 7, M5 = 31 and M7 = 127.A basic theorem about Mersenne numbers states that if Mp is prime, then the exponent p must also be prime. This follows from the identity
This rules out primality for Mersenne numbers with composite exponent, such as M4 = 24 − 1 = 15 = 3 × 5 = (22 − 1) × (1 + 22).
Though the above examples might suggest that Mp is prime for all primes p, this is not the case, and the smallest counterexample is the Mersenne number
M11 = 211 − 1 = 2047 = 23 × 89.The evidence at hand does suggest that a randomly selected Mersenne number is much more likely to be prime than an arbitrary randomly selected odd integer of similar size. Nonetheless, prime Mp appear to grow increasingly sparse as p increases. In fact, of the 2,270,720 prime numbers p up to 37,156,667, Mp is prime for only 45 of them.
The lack of any simple test to determine whether a given Mersenne number is prime makes the search for Mersenne primes a difficult task, since Mersenne numbers grow very rapidly. The Lucas–Lehmer primality test (LLT) is an efficient primality test that greatly aids this task. The search for the largest known prime has somewhat of a cult following. Consequently, a lot of computer power has been expended searching for new Mersenne primes, much of which is now done using distributed computing.
Mersenne primes are used in pseudorandom number generators such as the Mersenne twister, Park–Miller random number generator, Generalized Shift Register and Fibonacci RNG.
Perfect numbers
Mersenne primes Mp are also noteworthy due to their connection with perfect numbers. In the 4th century BC, Euclid proved that if 2p − 1 is prime, then 2p − 1(2p − 1) is a perfect number. This number, also expressible as Mp(Mp + 1)/2, is the Mpth triangular number and the 2p − 1th hexagonal number. In the 18th century, Leonhard Euler proved that, conversely, all even perfect numbers have this form. This is known as the Euclid–Euler theorem. It is unknown whether there are any odd perfect numbers.
History
Mersenne primes take their name from the 17th-century French scholar Marin Mersenne, who compiled what was supposed to be a list of Mersenne primes with exponents up to 257. The exponents listed by Mersenne were as follows:
His list was accurate through 31, but then became largely incorrect, as Mersenne mistakenly included M67 and M257 (which are composite) and omitted M61, M89, and M107 (which are prime). Mersenne gave little indication how he came up with his list.
Édouard Lucas proved in 1876 that M127 is indeed prime, as Mersenne claimed. This was the largest known prime number for 75 years, and the largest ever found by hand. M61 was determined to be prime in 1883 by Ivan Mikheevich Pervushin, though Mersenne claimed it was composite, and for this reason it is sometimes called Pervushin's number. This was the second-largest known prime number, and it remained so until 1911. Lucas had shown another error in Mersenne's list in 1876. Without finding a factor, Lucas demonstrated that M67 is actually composite. No factor was found until a famous talk by Frank Nelson Cole in 1903. Without speaking a word, he went to a blackboard and raised 2 to the 67th power, then subtracted one. On the other side of the board, he multiplied 193,707,721 × 761,838,257,287 and got the same number, then returned to his seat (to applause) without speaking. He later said that the result had taken him "three years of Sundays" to find. A correct list of all Mersenne primes in this number range was completed and rigorously verified only about three centuries after Mersenne published his list.
Searching for Mersenne primes
Fast algorithms for finding Mersenne primes are available, and as of 2016 the six largest known prime numbers are Mersenne primes.
The first four Mersenne primes M2 = 3, M3 = 7, M5 = 31 and M7 = 127 were known in antiquity. The fifth, M13 = 8191, was discovered anonymously before 1461; the next two (M17 and M19) were found by Pietro Cataldi in 1588. After nearly two centuries, M31 was verified to be prime by Leonhard Euler in 1772. The next (in historical, not numerical order) was M127, found by Édouard Lucas in 1876, then M61 by Ivan Mikheevich Pervushin in 1883. Two more (M89 and M107) were found early in the 20th century, by R. E. Powers in 1911 and 1914, respectively.
The best method presently known for testing the primality of Mersenne numbers is the Lucas–Lehmer primality test. Specifically, it can be shown that for prime p > 2, Mp = 2p − 1 is prime if and only if Mp divides Sp − 2, where S0 = 4 and Sk = (Sk − 1)2 − 2 for k > 0.
During the era of manual calculation, all the exponents up to and including 257 were tested with the Lucas–Lehmer test and found to be composite. A notable contribution was made by retired Yale physics professor Horace Scudder Uhler, who did the calculations for exponents 157, 167, 193, 199, 227, and 229. Unfortunately for those investigators, the interval they were testing contains the largest known gap between Mersenne primes, in relative terms: the next prime exponent would turn out to be more than four times larger than the previous record of 127.
The search for Mersenne primes was revolutionized by the introduction of the electronic digital computer. Alan Turing searched for them on the Manchester Mark 1 in 1949, but the first successful identification of a Mersenne prime, M521, by this means was achieved at 10:00 pm on January 30, 1952 using the U.S. National Bureau of Standards Western Automatic Computer (SWAC) at the Institute for Numerical Analysis at the University of California, Los Angeles, under the direction of Lehmer, with a computer search program written and run by Prof. R. M. Robinson. It was the first Mersenne prime to be identified in thirty-eight years; the next one, M607, was found by the computer a little less than two hours later. Three more — M1279, M2203, M2281 — were found by the same program in the next several months. M4253 is the first Mersenne prime that is titanic, M44,497 is the first gigantic, and M6,972,593 was the first megaprime to be discovered, being a prime with at least 1,000,000 digits. All three were the first known prime of any kind of that size. The number of digits in the decimal representation of Mn equals ⌊n × log102⌋ + 1, where ⌊x⌋ denotes the floor function (or equivalently ⌊log10Mn⌋ + 1).
In September 2008, mathematicians at UCLA participating in GIMPS won part of a $100,000 prize from the Electronic Frontier Foundation for their discovery of a very nearly 13-million-digit Mersenne prime. The prize, finally confirmed in October 2009, is for the first known prime with at least 10 million digits. The prime was found on a Dell OptiPlex 745 on August 23, 2008. This was the eighth Mersenne prime discovered at UCLA.
On April 12, 2009, a GIMPS server log reported that a 47th Mersenne prime had possibly been found. The find was verified on June 12, 2009. The prime is 242,643,801 − 1. Although it is chronologically the 47th Mersenne prime to be discovered, it is smaller than the largest known at the time, which was the 45th to be discovered.
On January 25, 2013, Curtis Cooper, a mathematician at the University of Central Missouri, discovered a 48th Mersenne prime, 257,885,161 − 1 (a number with 17,425,170 digits), as a result of a search executed by a GIMPS server network.
On January 19, 2016, Cooper published his discovery of a 49th Mersenne prime, 274,207,281 − 1 (a number with 22,338,618 digits), as a result of a search executed by a GIMPS server network. This was the fourth Mersenne prime discovered by Cooper and his team in the past ten years.
Theorems about Mersenne numbers
- If a and p are natural numbers such that ap − 1 is prime, then a = 2 or p = 1.
- Proof: a ≡ 1 (mod a − 1). Then ap ≡ 1 (mod a − 1), so ap − 1 ≡ 0 (mod a − 1). Thus a − 1 | ap − 1. However, ap − 1 is prime, so a − 1 = ap − 1 or a − 1 = ±1. In the former case, a = ap, hence a = 0,1 (which is a contradiction, as neither −1 nor 0 is prime) or p = 1. In the latter case, a = 2 or a = 0. If a = 0, however, 0p − 1 = 0 − 1 = −1 which is not prime. Therefore, a = 2.
- If 2p − 1 is prime, then p is prime.
- Proof: suppose that p is composite, hence can be written p = ab with a and b > 1. Then 2p − 1 = 2ab − 1 = (2a)b − 1 = (2a − 1)((2a)b − 1 + (2a)b − 2 + … + 2a + 1) so 2p − 1 is composite contradicting our assumption that 2p − 1 is prime.
- If p is an odd prime, then every prime q that divides 2p − 1 must be 1 plus a multiple of 2p. This holds even when 2p − 1 is prime.
- Examples: Example I: 25 − 1 = 31 is prime, and 31 = 1 + 3 × (2 × 5). Example II: 211 − 1 = 23 × 89, where 23 = 1 + (2 × 11), and 89 = 1 + 4 × (2 × 11).
- Proof: By Fermat's little theorem, q is a factor of 2q − 1 − 1. Since q is a factor of 2p − 1, for all positive integers c, q is also a factor of 2pc − 1. Since p is prime and q is not a factor of 21 − 1, p is also the smallest positive integer x such that q is a factor of 2x − 1. As a result, for all positive integers x, q is a factor of 2x − 1 if and only if p is a factor of x. Therefore, since q is a factor of 2q − 1 − 1, p is a factor of q − 1 so q ≡ 1 (mod p). Furthermore, since q is a factor of 2p − 1, which is odd, q is odd. Therefore, q ≡ 1 (mod 2p).
- Note: This fact provides a proof of Euclid's theorem, which asserts the infinitude of primes, distinct from the proof written by Euclid: for every odd prime p, all primes dividing 2p − 1 are larger than p; thus there are always larger primes than any particular prime.
- Note: In conjunction with the next theorem below, certain multiples of 2p are impossible, namely when 2p is multiplied by twice an odd number. Thus for instance 4p+1, 12p+1, 20p+1, and so forth cannot be factors of 2p − 1. Proof: Each factor must have 2kp + 1 = 8n ± 1 for some k and n, so if we assume k = 2(2m+1) then we get either p = 2(n−mp) or 2p + 1 = 4(n−mp), each of which is a contradiction as one side of the equation is odd and the other is even. More generally we can show that (p mod 4) ≡ 1 ⇒ k ≡ 0 or 3 (mod 4), and (p mod 4) ≡ 3 ⇒ k ≡ 0 or 1 (mod 4).
- If p is an odd prime, then every prime q that divides 2p − 1 is congruent to ±1 (mod 8).
- Proof: 2p + 1 ≡ 2 (mod q), so 21/2(p + 1) is a square root of 2 mod q. By quadratic reciprocity, every prime modulo in which the number 2 has a square root is congruent to ±1 (mod 8).
- A Mersenne prime cannot be a Wieferich prime.
- Proof: We show if p = 2m − 1 is a Mersenne prime, then the congruence 2p − 1 ≡ 1 (mod p2) does not hold. By Fermat's little theorem, m | p − 1. Now write, p − 1 = mλ. If the given congruence is satisfied, then p2 | 2mλ − 1,therefore 0 ≡ 2mλ − 1/2m − 1 = 1 + 2m + 22m + ... + 2(λ − 1)m ≡ −λ mod (2m − 1). Hence 2m − 1 | λ,and therefore λ ≥ 2m − 1. This leads to p − 1 ≥ m(2m − 1), which is impossible since m ≥ 2.
- If m and n are natural numbers then m and n are coprime if and only if 2m − 1 and 2n − 1 are coprime. Consequently, a prime number divides at most one prime-exponent Mersenne number, so in other words the set of pernicious Mersenne numbers is pairwise coprime.
- If p and 2p + 1 are both prime (meaning that p is a Sophie Germain prime), and p is congruent to 3 (mod 4), then 2p + 1 divides 2p − 1.
- Example: 11 and 23 are both prime, and 11 = 2 × 4 + 3, so 23 divides 211 − 1.
- Proof: Let q be 2p + 1. By Fermat's little theorem, 22p ≡ 1 (mod q), so either 2p ≡ 1 (mod q) or 2p ≡ −1 (mod q). Supposing latter true, then 2p + 1 = (21/2(p + 1))2 ≡ −2 (mod q), so −2 would be a quadratic residue mod q. However, since p is congruent to 3 (mod 4), q is congruent to 7 (mod 8) and therefore 2 is a quadratic residue mod q. Also since q is congruent to 3 (mod 4), −1 is a quadratic nonresidue mod q, so −2 is the product of a residue and a nonresidue and hence it is a nonresidue, which is a contradiction. Hence, the former congruence must be true and 2p + 1 divides Mp.
- All composite divisors of prime-exponent Mersenne numbers pass the Fermat primality test for the base 2.
List of known Mersenne primes
The table below lists all known Mersenne primes (sequence A000043 (p) and A000668 (Mp) in OEIS):
All Mersenne numbers below the 48th Mersenne prime (M57,885,161) have been tested at least once but some have not been double-checked. Primes are not always discovered in increasing order. For example, the 29th Mersenne prime was discovered after the 30th and the 31st. Similarly, M43,112,609 was followed by two smaller Mersenne primes, first 2 weeks later and then 8 months later.
The largest known Mersenne prime (274,207,281 − 1) is also the largest known prime number. To help visualize its size, displaying the number in base 10 would require 5,957 pages with 75 digits per line and 50 lines per page. M43,112,609 was the first discovered prime number with more than 10 million decimal digits.
In modern times, the largest known prime has almost always been a Mersenne prime.
Factorization of composite Mersenne numbers
The factors of a prime number are by definition one, and the number itself – this section is about composite numbers. Mersenne numbers are very good test cases for the special number field sieve algorithm, so often the largest number factorized with this algorithm has been a Mersenne number. As of August 2016, 21,193 − 1 is the record-holder, using a variant on the special number field sieve allowing the factorisation of several numbers at once. See integer factorization records for links to more information. The special number field sieve can factorize numbers with more than one large factor. If a number has only one very large factor then other algorithms can factorize larger numbers by first finding small factors and then making a primality test on the cofactor. As of August 2016, the largest factorization with probable prime factors allowed is 25,240,707 − 1 = 75,392,810,903 × q, where q is a 1,577,600-digit probable prime.
(sequence A244453 in the OEIS) (or A089162 with both prime and composite Mersenne numbers) (for the primes p, see A054723)
Mersenne primitive part
The primitive part of Mersenne number Mn is Φn(2), the nth cyclotomic polynomial at 2, they are
1, 3, 7, 5, 31, 3, 127, 17, 73, 11, 2047, 13, 8191, 43, 151, 257, 131071, 57, 524287, 205, 2359, 683, 8388607, 241, 1082401, 2731, 262657, 3277, 536870911, 331, ... (sequence A019320 in the OEIS)Besides, if we notice those prime factors, and delete "old prime factors", for example, 3 divides the 2nd, 6th, 18th, 54th, 162nd, ... terms of this sequence, we only allow the 2nd term divided by 3, if we do, they are
1, 3, 7, 5, 31, 1, 127, 17, 73, 11, 2047, 13, 8191, 43, 151, 257, 131071, 19, 524287, 41, 337, 683, 8388607, 241, 1082401, 2731, 262657, 3277, 536870911, 331, ... (sequence A064078 in the OEIS)The numbers n for which Φn(2) is prime are
2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 19, 22, 24, 26, 27, 30, 31, 32, 33, 34, 38, 40, 42, 46, 49, 56, 61, 62, 65, 69, 77, 78, 80, 85, 86, 89, 90, 93, 98, 107, 120, 122, 126, 127, 129, 133, 145, 150, ... (sequence A072226 in the OEIS)The numbers n for which 2n − 1 has an only primitive prime factor are
2, 3, 4, 5, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 24, 26, 27, 30, 31, 32, 33, 34, 38, 40, 42, 46, 49, 54, 56, 61, 62, 65, 69, 77, 78, 80, 85, 86, 89, 90, 93, 98, 107, 120, 122, 126, 127, 129, 133, 145, 147, 150, ... (sequence A161508 in the OEIS) (Differ from last sequence, this sequence does not have the term 6, but has the terms 18, 20, 21, 54, 147, 342, 602, and 889, and it is conjectured that no others)Mersenne numbers in nature and elsewhere
In computer science, unsigned n-bit integers can be used to express numbers up to Mn. Signed (n + 1)-bit integers can express values between −(Mn + 1) and Mn, using the two's complement representation.
In the mathematical problem Tower of Hanoi, solving a puzzle with an n-disc tower requires Mn steps, assuming no mistakes are made.
The asteroid with minor planet number 8191 is named 8191 Mersenne after Marin Mersenne, because 8191 is a Mersenne prime (3 Juno, 7 Iris, 31 Euphrosyne and 127 Johanna having been discovered and named during the 19th century).
Mersenne–Fermat primes
A Mersenne–Fermat number is defined as 2pr − 1/2pr − 1 − 1, with p prime, r natural number, and can be written as MF(p, r), when r = 1, it is a Mersenne number, and when p = 2, it is a Fermat number, the only known Mersenne–Fermat prime with r > 1 are
MF(2, 2), MF(3, 2), MF(7, 2), MF(59, 2), MF(2, 3), MF(3, 3), MF(2, 4), and MF(2, 5).In fact, MF(p, r) = Φpr(2), where Φ is the cyclotomic polynomial.
Generalizations
The simplest generalized Mersenne primes are prime numbers of the form f(2n), where f(x) is a low-degree polynomial with small integer coefficients. An example is 264 − 232 + 1, in this case, n = 32, and f(x) = x2 − x + 1; another example is 2192 − 264 − 1, in this case, n = 64, and f(x) = x3 − x − 1.
It is also natural to try to generalize primes of the form 2n − 1 to primes of the form bn − 1 (for b ≠ 2 and n > 1). However (see also theorems above), bn − 1 is always divisible by b − 1, so unless the latter is a unit, the former is not a prime. There are two ways to deal with that:
Complex numbers
In the ring of integers (on real numbers), if b − 1 is a unit, then b is either 2 or 0. But 2n − 1 are the usual Mersenne primes, and the formula 0n − 1 does not lead to anything interesting (since it is always −1 for all n > 0). Thus, we can regard a ring of "integers" on complex numbers instead of real numbers, like Gaussian integers and Eisenstein integers.
Gaussian Mersenne primes
If we regard the ring of Gaussian integers, we get the case b = 1 + i and b = 1 − i, and can ask (WLOG) for what n the number (1 + i)n − 1 is a Gaussian prime which will then be called a Gaussian Mersenne prime.
(1 + i)n − 1 is a Gaussian prime for the following n:
2, 3, 5, 7, 11, 19, 29, 47, 73, 79, 113, 151, 157, 163, 167, 239, 241, 283, 353, 367, 379, 457, 997, 1367, 3041, 10141, 14699, 27529, 49207, 77291, 85237, 106693, 160423, 203789, 364289, 991961, 1203793, 1667321, 3704053, 4792057, ... (sequence A057429 in the OEIS)This sequence is in many ways similar to the list of exponents of ordinary Mersenne primes.
The norms (i.e. squares of absolute values) of these Gaussian primes are rational primes:
5, 13, 41, 113, 2113, 525313, 536903681, 140737471578113, ... (sequence A182300 in the OEIS).Eisenstein Mersenne primes
We can also regard the ring of Eisenstein integers, we get the case b = 1 + ω and b = 1 − ω, and can ask for what n the number (1 + ω)n − 1 is an Eisenstein prime which will then be called a Eisenstein Mersenne prime.
(1 + ω)n − 1 is an Eisenstein prime for the following n:
2, 5, 7, 11, 17, 19, 79, 163, 193, 239, 317, 353, 659, 709, 1049, 1103, 1759, 2029, 5153, 7541, 9049, 10453, 23743, 255361, 534827, 2237561, ... (sequence A066408 in the OEIS)The norms (i.e. squares of absolute values) of these Eisenstein primes are rational primes:
7, 271, 2269, 176419, 129159847, 1162320517, ... (sequence A066413 in the OEIS)Repunit primes
The other way to deal with the fact that bn − 1 is always divisible by b − 1, it is to simply take out this factor and ask which values of n make
be prime. (The integer b can be either positive or negative.) If for example we take b = 10, we get n values of:
2, 19, 23, 317, 1031, 49081, 86453, 109297, 270343, ... (sequence A004023 in the OEIS),corresponding to primes 11, 1111111111111111111, 11111111111111111111111, ... (sequence A004022 in the OEIS).
These primes are called repunit primes. Another example is when we take b = −12, we get n values of:
2, 5, 11, 109, 193, 1483, 11353, 21419, 21911, 24071, 106859, 139739, ... (sequence A057178 in the OEIS),corresponding to primes −11, 19141, 57154490053, ....
It is a conjecture that for every integer b which is not a perfect power, there are infinitely many values of n such that bn − 1/b − 1 is prime. (When b is a perfect power, it can be shown that there is at most one n value such that bn − 1/b − 1 is prime)
Least n such that bn − 1/b − 1 is prime are (starting with b = 2)
2, 3, 2, 3, 2, 5, 3, 0, 2, 17, 2, 5, 3, 3, 2, 3, 2, 19, 3, 3, 2, 5, 3, 0, 7, 3, 2, 5, 2, 7, 0, 3, 13, 313, 2, 13, 3, 349, 2, 3, 2, 5, 5, 19, 2, 127, 19, 0, 3, 4229, 2, 11, 3, 17, 7, 3, 2, 3, 2, 7, 3, 5, 0, 19, 2, 19, 5, 3, 2, 3, 2, ... (sequence A084740 in the OEIS)For negative bases b, they are (starting with b = −2)
3, 2, 2, 5, 2, 3, 2, 3, 5, 5, 2, 3, 2, 3, 3, 7, 2, 17, 2, 3, 3, 11, 2, 3, 11, 0, 3, 7, 2, 109, 2, 5, 3, 11, 31, 5, 2, 3, 53, 17, 2, 5, 2, 103, 7, 5, 2, 7, 1153, 3, 7, 21943, 2, 3, 37, 53, 3, 17, 2, 7, 2, 3, 0, 19, 7, 3, 2, 11, 3, 5, 2, ... (sequence A084742 in the OEIS) (notice this OEIS sequence does not allow n = 2)Least base b such that bprime(n) − 1/b − 1 is prime are
2, 2, 2, 2, 5, 2, 2, 2, 10, 6, 2, 61, 14, 15, 5, 24, 19, 2, 46, 3, 11, 22, 41, 2, 12, 22, 3, 2, 12, 86, 2, 7, 13, 11, 5, 29, 56, 30, 44, 60, 304, 5, 74, 118, 33, 156, 46, 183, 72, 606, 602, 223, 115, 37, 52, 104, 41, 6, 338, 217, ... (sequence A066180 in the OEIS)For negative bases b, they are
3, 2, 2, 2, 2, 2, 2, 2, 2, 7, 2, 16, 61, 2, 6, 10, 6, 2, 5, 46, 18, 2, 49, 16, 70, 2, 5, 6, 12, 92, 2, 48, 89, 30, 16, 147, 19, 19, 2, 16, 11, 289, 2, 12, 52, 2, 66, 9, 22, 5, 489, 69, 137, 16, 36, 96, 76, 117, 26, 3, ... (sequence A103795 in the OEIS)Other generalized Mersenne primes
Another generalized Mersenne number is
with a, b any coprime integers, a > 1 and −a < b < a. (Since an − bn is always divisible by a − b, the division is necessary for there to be any chance of finding prime numbers. In fact, this number is the same as the Lucas number Un(a + b, ab), since a and b are the roots of the quadratic equation x2 − (a + b)x + ab = 0, and this number equals 1 when n = 1) We can ask which n makes this number prime. It can be shown that such n must be primes themselves or equal to 4, and n can be 4 if and only if a + b = 1 and a2 + b2 is prime. (Since a4 − b4/a − b = (a + b)(a2 + b2). Thus, in this case the pair (a, b) must be (x + 1, −x) and x2 + (x + 1)2 must be prime. That is, x must be in A027861.) It is a conjecture that for any pair (a, b) such that for every natural number r > 1, a and b are not both perfect rth powers, and −4ab is not a perfect fourth power. there are infinitely many values of n such that an − bn/a − b is prime. (When a and b are both perfect rth powers for an r > 1 or when −4ab is a perfect fourth power, it can be shown that there are at most two n values with this property, since if so, then an − bn/a − b can be factored algebraically) However, this has not been proved for any single value of (a, b).
*Note: if b < 0 and n is even, then the numbers n are not included in the corresponding OEIS sequence.
A conjecture related to the generalized Mersenne primes: (the conjecture predicts where is the next generalized Mersenne prime, if the conjecture is true, then there are infinitely many primes for all such (a,b) pairs)
For any integers a and b which satisfy the conditions:
- a > 1, −a < b < a.
- a and b are coprime. (thus, b cannot be 0)
- For every natural number r > 1, a and b are not both perfect rth powers. (since when a and b are both perfect rth powers, it can be shown that there are at most two n value such that an − bn/a − b is prime, and these n values are r itself or a root of r, or 2)
- −4ab is not a perfect fourth power (if so, then the number has aurifeuillean factorization).
has prime numbers of the form
for prime p, the prime numbers will be distributed near the best fit line
where
and there are about
prime numbers of this form less than N.
We also have the following three properties:
- The number of prime numbers of the form ap − bp/a − b (with prime p) less than or equal to n is about eγ loga(loga(n)).
- The expected number of prime numbers of the form ap − bp/a − b with prime p between n and an is about eγ.
- The probability that number of the form ap − bp/a − b is prime (for prime p) is about eγ/p loge(a).
If this conjecture is true, then for all such (a,b) pairs, let q be the nth prime of the form ap − bp/a − b, the graph of loga(loga(q)) versus n is almost linear. (See )
When a = b + 1, it is (b + 1)n − bn, a difference of two consecutive perfect nth powers, and if an − bn is prime, then a must be b + 1, because it is divisible by a − b.
Least n such that (b + 1)n − bn is prime are
2, 2, 2, 3, 2, 2, 7, 2, 2, 3, 2, 17, 3, 2, 2, 5, 3, 2, 5, 2, 2, 229, 2, 3, 3, 2, 3, 3, 2, 2, 5, 3, 2, 3, 2, 2, 3, 3, 2, 7, 2, 3, 37, 2, 3, 5, 58543, 2, 3, 2, 2, 3, 2, 2, 3, 2, 5, 3, 4663, 54517, 17, 3, 2, 5, 2, 3, 3, 2, 2, 47, 61, 19, ... (sequence A058013 in the OEIS)Least b such that (b + 1)prime(n) − bprime(n) is prime are
1, 1, 1, 1, 5, 1, 1, 1, 5, 2, 1, 39, 6, 4, 12, 2, 2, 1, 6, 17, 46, 7, 5, 1, 25, 2, 41, 1, 12, 7, 1, 7, 327, 7, 8, 44, 26, 12, 75, 14, 51, 110, 4, 14, 49, 286, 15, 4, 39, 22, 109, 367, 22, 67, 27, 95, 80, 149, 2, 142, 3, 11, ... (sequence A222119 in the OEIS)