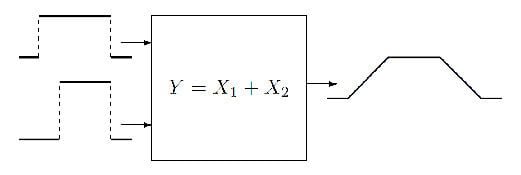Measurement uncertainty

Background

The purpose of measurement is to provide information about a quantity of interest – a measurand. For example, the measurand might be the size of a cylindrical feature, the volume of a vessel, the potential difference between the terminals of a battery, or the mass concentration of lead in a flask of water.

No measurement is exact. When a quantity is measured, the outcome depends on the measuring system, the measurement procedure, the skill of the operator, the environment, and other effects. Even if the quantity were to be measured several times, in the same way and in the same circumstances, a different measured value would in general be obtained each time, assuming the measuring system has sufficient resolution to distinguish between the values.

The dispersion of the measured values would relate to how well the measurement is performed. Their average would provide an estimate of the true value of the quantity that generally would be more reliable than an individual measured value. The dispersion and the number of measured values would provide information relating to the average value as an estimate of the true value. However, this information would not generally be adequate.

The measuring system may provide measured values that are not dispersed about the true value, but about some value offset from it. Take a domestic bathroom scale. Suppose it is not set to show zero when there is nobody on the scale, but to show some value offset from zero. Then, no matter how many times the person's mass were re-measured, the effect of this offset would be inherently present in the average of the values.

Measurement uncertainty has important economic consequences for calibration and measurement activities. In calibration reports, the magnitude of the uncertainty is often taken as an indication of the quality of the laboratory, and smaller uncertainty values generally are of higher value and of higher cost. The American Society of Mechanical Engineers (ASME) has produced a suite of standards addressing various aspects of measurement uncertainty. ASME B89.7.3.1, Guidelines for Decision Rules in Determining Conformance to Specifications addresses the role of measurement uncertainty when accepting or rejecting products based on a measurement result and a product specification. ASME B89.7.3.2, Guidelines for the Evaluation of Dimensional Measurement Uncertainty, provides a simplified approach (relative to the GUM) to the evaluation of dimensional measurement uncertainty. ASME B89.7.3.3, Guidelines for Assessing the Reliability of Dimensional Measurement Uncertainty Statements, examines how to resolve disagreements over the magnitude of the measurement uncertainty statement. ASME B89.7.4, Measurement Uncertainty and Conformance Testing: Risk Analysis, provides guidance on the risks involved in any product acceptance/rejection decision.

The "Guide to the Expression of Uncertainty in Measurement", commonly known as the GUM, is the definitive document on this subject. The GUM has been adopted by all major National Measurement Institutes (NMIs), by international laboratory accreditation standards such as ISO/IEC 17025 General requirements for the competence of testing and calibration laboratories which is required for international laboratory Accreditation, and employed in most modern national and international documentary standards on measurement methods and technology. See Joint Committee for Guides in Metrology.

Indirect measurement

The above discussion concerns the direct measurement of a quantity, which incidentally occurs rarely. For example, the bathroom scale may convert a measured extension of a spring into an estimate of the measurand, the mass of the person on the scale. The particular relationship between extension and mass is determined by the calibration of the scale. A measurement model converts a quantity value into the corresponding value of the measurand.

There are many types of measurement in practice and therefore many models. A simple measurement model (for example for a scale, where the mass is proportional to the extension of the spring) might be sufficient for everyday domestic use. Alternatively, a more sophisticated model of a weighing, involving additional effects such as air buoyancy, is capable of delivering better results for industrial or scientific purposes. In general there are often several different quantities, for example temperature, humidity and displacement, that contribute to the definition of the measurand, and that need to be measured.

Correction terms should be included in the measurement model when the conditions of measurement are not exactly as stipulated. These terms correspond to systematic errors. Given an estimate of a correction term, the relevant quantity should be corrected by this estimate. There will be an uncertainty associated with the estimate, even if the estimate is zero, as is often the case. Instances of systematic errors arise in height measurement, when the alignment of the measuring instrument is not perfectly vertical, and the ambient temperature is different from that prescribed. Neither the alignment of the instrument nor the ambient temperature is specified exactly, but information concerning these effects is available, for example the lack of alignment is at most 0.001° and the ambient temperature at the time of measurement differs from that stipulated by at most 2 °C.

As well as raw data representing measured values, there is another form of data that is frequently needed in a measurement model. Some such data relate to quantities representing physical constants, each of which is known imperfectly. Examples are material constants such as modulus of elasticity and specific heat. There are often other relevant data given in reference books, calibration certificates, etc., regarded as estimates of further quantities.

The items required by a measurement model to define a measurand are known as input quantities in a measurement model. The model is often referred to as a functional relationship. The output quantity in a measurement model is the measurand.

Formally, the output quantity, denoted by Y , about which information is required, is often related to input quantities, denoted by X 1 , … , X N , about which information is available, by a measurement model in the form of

where f is known as the measurement function. A general expression for a measurement model is

It is taken that a procedure exists for calculating Y given X 1 , … , X N , and that Y is uniquely defined by this equation.

Propagation of distributions

The true values of the input quantities X 1 , … , X N are unknown. In the GUM approach, X 1 , … , X N are characterized by probability distributions and treated mathematically as random variables. These distributions describe the respective probabilities of their true values lying in different intervals, and are assigned based on available knowledge concerning X 1 , … , X N . Sometimes, some or all of X 1 , … , X N are interrelated and the relevant distributions, which are known as joint, apply to these quantities taken together.

Consider estimates x 1 , … , x N , respectively, of the input quantities X 1 , … , X N , obtained from certificates and reports, manufacturers' specifications, the analysis of measurement data, and so on. The probability distributions characterizing X 1 , … , X N are chosen such that the estimates x 1 , … , x N , respectively, are the expectations of X 1 , … , X N . Moreover, for the i th input quantity, consider a so-called standard uncertainty, given the symbol u ( x i ) , defined as the standard deviation of the input quantity X i . This standard uncertainty is said to be associated with the (corresponding) estimate x i .

The use of available knowledge to establish a probability distribution to characterize each quantity of interest applies to the X i and also to Y . In the latter case, the characterizing probability distribution for Y is determined by the measurement model together with the probability distributions for the X i . The determination of the probability distribution for Y from this information is known as the propagation of distributions.

The figure below depicts a measurement model Y = X 1 + X 2 in the case where X 1 and X 2 are each characterized by a (different) rectangular, or uniform, probability distribution. Y has a symmetric trapezoidal probability distribution in this case.

Once the input quantities X 1 , … , X N have been characterized by appropriate probability distributions, and the measurement model has been developed, the probability distribution for the measurand Y is fully specified in terms of this information. In particular, the expectation of Y is used as the estimate of Y , and the standard deviation of Y as the standard uncertainty associated with this estimate.

Often an interval containing Y with a specified probability is required. Such an interval, a coverage interval, can be deduced from the probability distribution for Y . The specified probability is known as the coverage probability. For a given coverage probability, there is more than one coverage interval. The probabilistically symmetric coverage interval is an interval for which the probabilities (summing to one minus the coverage probability) of a value to the left and the right of the interval are equal. The shortest coverage interval is an interval for which the length is least over all coverage intervals having the same coverage probability.

Prior knowledge about the true value of the output quantity Y can also be considered. For the domestic bathroom scale, the fact that the person's mass is positive, and that it is the mass of a person, rather than that of a motor car, that is being measured, both constitute prior knowledge about the possible values of the measurand in this example. Such additional information can be used to provide a probability distribution for Y that can give a smaller standard deviation for Y and hence a smaller standard uncertainty associated with the estimate of Y .

Type A and Type B evaluation of uncertainty

Knowledge about an input quantity X i is inferred from repeated measured values ("Type A evaluation of uncertainty"), or scientific judgement or other information concerning the possible values of the quantity ("Type B evaluation of uncertainty").

In Type A evaluations of measurement uncertainty, the assumption is often made that the distribution best describing an input quantity X given repeated measured values of it (obtained independently) is a Gaussian distribution. X then has expectation equal to the average measured value and standard deviation equal to the standard deviation of the average. When the uncertainty is evaluated from a small number of measured values (regarded as instances of a quantity characterized by a Gaussian distribution), the corresponding distribution can be taken as a t-distribution. Other considerations apply when the measured values are not obtained independently.

For a Type B evaluation of uncertainty, often the only available information is that X lies in a specified interval [ a , b ]. In such a case, knowledge of the quantity can be characterized by a rectangular probability distribution with limits a and b . If different information were available, a probability distribution consistent with that information would be used.

Sensitivity coefficients

Sensitivity coefficients c 1 , … , c N describe how the estimate y of Y would be influenced by small changes in the estimates x 1 , … , x N of the input quantities X 1 , … , X N . For the measurement model Y = f ( X 1 , … , X N ) , the sensitivity coefficient c i equals the partial derivative of first order of f with respect to X i evaluated at X 1 = x 1 , X 2 = x 2 , etc. For a linear measurement model

with X 1 , … , X N independent, a change in x i equal to u ( x i ) would give a change c i u ( x i ) in y . This statement would generally be approximate for measurement models Y = f ( X 1 , … , X N ) . The relative magnitudes of the terms | c i | u ( x i ) are useful in assessing the respective contributions from the input quantities to the standard uncertainty u ( y ) associated with y .

The standard uncertainty u ( y ) associated with the estimate y of the output quantity Y is not given by the sum of the | c i | u ( x i ) , but these terms combined in quadrature, namely by [an expression that is generally approximate for measurement models Y = f ( X 1 , … , X N ) ]

which is known as the law of propagation of uncertainty.

When the input quantities X i contain dependencies, the above formula is augmented by terms containing covariances, which may increase or decrease u ( y ) .

Uncertainty evaluation

The main stages of uncertainty evaluation constitute formulation and calculation, the latter consisting of propagation and summarizing. The formulation stage constitutes

1. defining the output quantity Y (the measurand),
2. identifying the input quantities on which Y depends,
3. developing a measurement model relating Y to the input quantities, and
4. on the basis of available knowledge, assigning probability distributions — Gaussian, rectangular, etc. — to the input quantities (or a joint probability distribution to those input quantities that are not independent).

The calculation stage consists of propagating the probability distributions for the input quantities through the measurement model to obtain the probability distribution for the output quantity Y , and summarizing by using this distribution to obtain

1. the expectation of Y , taken as an estimate y of Y ,
2. the standard deviation of Y , taken as the standard uncertainty u ( y ) associated with y , and
3. a coverage interval containing Y with a specified coverage probability.

The propagation stage of uncertainty evaluation is known as the propagation of distributions, various approaches for which are available, including

1. the GUM uncertainty framework, constituting the application of the law of propagation of uncertainty, and the characterization of the output quantity Y by a Gaussian or a t -distribution,
2. analytic methods, in which mathematical analysis is used to derive an algebraic form for the probability distribution for Y , and
3. a Monte Carlo method, in which an approximation to the distribution function for Y is established numerically by making random draws from the probability distributions for the input quantities, and evaluating the model at the resulting values.

For any particular uncertainty evaluation problem, approach 1), 2) or 3) (or some other approach) is used, 1) being generally approximate, 2) exact, and 3) providing a solution with a numerical accuracy that can be controlled.

Models with any number of output quantities

When the measurement model is multivariate, that is, it has any number of output quantities, the above concepts can be extended. The output quantities are now described by a joint probability distribution, the coverage interval becomes a coverage region, the law of propagation of uncertainty has a natural generalization, and a calculation procedure that implements a multivariate Monte Carlo method is available.

Alternative perspective

Most of this article represents the most common view of measurement uncertainty, which assumes that random variables are proper mathematical models for uncertain quantities and simple probability distributions are sufficient for representing all forms of measurement uncertainties. In some situations, however, a mathematical interval rather than a probability distribution might be a better model of uncertainty. This may include situations involving periodic measurements, binned data values, censoring, detection limits, or plus-minus ranges of measurements where no particular probability distribution seems justified or where one cannot assume that the errors among individual measurements are completely independent.

A more robust representation of measurement uncertainty in such cases can be fashioned from intervals. An interval [a,b] is different from a rectangular or uniform probability distribution over the same range in that the latter suggests that the true value lies inside the right half of the range [(a + b)/2, b] with probability one half, and within any subinterval of [a,b] with probability equal to the width of the subinterval divided by b – a. The interval makes no such claims, except simply that the measurement lies somewhere within the interval. Distributions of such measurement intervals can be summarized as probability boxes and Dempster–Shafer structures over the real numbers, which incorporate both aleatoric and epistemic uncertainties.